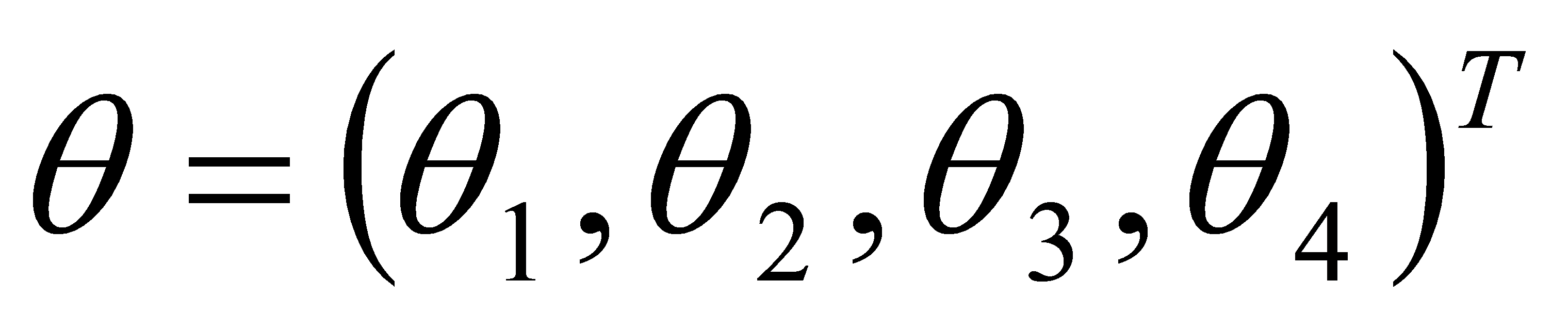5. fejezet - Adaptív szabályozás
Vissza		Előre

5. fejezet - Adaptív szabályozás

Tartalom

5.1. Az adaptív szabalyozas rövid története

A mindennapi nyelvhasználatban az "adaptálni" szó jelentése: a viselkedést megváltoztatni, alkalmazkodni az új körülményekhez vagy új állapotokhoz. Ezen értelmezés szerint az a szabályozó tekinthető adaptív szabályozónak, amely képes a viselkedését módosítani, megváltoztatni, válaszolva a folyamat dinamikájának változására, valamint a zavarokra. Mivel a közönséges visszacsatolt rendszer is hasonló megfontolásokból bevezették be, ezért azonnal felmerül az adaptív szabályozás és a visszacsatolt szabályozás közötti különbség kérdése. Évekig sok próbálkozás történt az adaptív szabályozás definiálására. Ezek az erőfeszítések azonban széles körben nem váltak elfogadottá. Hiányzik tehát az adaptív szabályozásoknak egy olyan pontos definíciója, amely lehetővé tenné egy szabályozó hardverének és szoftverének vizsgálatát és eldöntené azt, hogy adaptív-e vagy sem.

Gyakorlatilag azonban mégis szükséges állást foglalni az adaptív szabályozásokról. Ezért az mondható, hogy az adaptív szabályozás a nemlineáris visszacsatolt szabályozások speciális fajtája, amelyben a folyamatok állapotát olyan két kategóriára lehet szétválasztani, amelyek különböző mértékben változnak. A lassú változási állapotok úgy tekintők, mint paraméterek. Mindez két időskála gondolatával bemutatható: a gyorsabb időskála a közönséges visszacsatolást jelképezi, a lassabb a szabályozó paramétereinek megváltoztatását mutatja.

Néhány szóban az adaptív szabályozás történetéről és létrejöttéről: az 1950-es évek elején az adaptív szabályozás széles körű kutatása folyt nagyteljesítményű repülőgépek robotpilótáinak tervezésével kapcsolatban. Az ilyen repülőgépek széles sebesség- és magasságtartományban üzemelnek. Úgy találták, hogy a konstans körerősítéses, lineáris, visszacsatolt szabályozók képesek voltak egy működési állapotban jól működni, de ahogy ezek a működési viszonyok megváltoztak, úgy már nem voltak képesek az előírt jellemzőket tartani. Ezért szükség volt egy olyan igényesebb szabályozóra, amely képes a változó működési viszonyok széles tartományában megfelelően üzemelni. A tárgyban azonban az érdeklődés egyre inkább csökkent, köszönhetően a kutatásokba való bepillantás hiányának, valamint a repülési teszteknél történt szerencsétlenségeknek.

Azonban az 1960-as években számos új közlemények jelentek meg a szabályozási elmélettel kapcsolatban, amelyek hozzájárultak az adaptív szabályozás fejlődéséhez. Ilyen közlemények jelentek meg az állapottér és a stabilitás elméletében. Fontos eredmény volt a sztochasztikus szabályozás elméletének megjelenése.

Az 1970-es években volt az adaptív szabályozások reneszánsza, amikor is a különböző becslési eljárásokat a különféle tervezési módszerekkel kombinálták. Sok felhasználásról jelent meg beszámoló, de az elméleti eredmények nagyon korlátozottak voltak.

Az 1980-as évek elején megjelentek az adaptív szabályozás stabilitásának megfelelő bizonyítékai, bár nagyon korlátozó feltételezések mellett. Ezek azonban ismét felkeltették az érdeklődést az adaptív szabályozás robosztusságának, kutatása, valamint az univerzálisan stabilis szabályozások kutatása iránt. A mikroelektronika gyors és forradalmi fejlődése megteremtette a lehetőségét annak, hogy adaptív szabályozókat egyszerűen és olcsón tudjunk megalkotni. A különböző elgondolásokon alapuló kommersz adaptív szabályozók már a piacon is megjelentek és ipari felhasználásuk is jelentősen növekedik, illetve várhatóan növekedni fog a jövőben is. A terület erőteljes fejlődése napjainkban is történik, mind az egyetemi kutatólaboratóriumokban, mind az iparban, de az adaptív szabályozás még közel sem jelent teljesen átgondolt és lezárt elméletet.

5.2. Adaptív szabályozók felépítése

Ebben a részben összefoglaló jelleggel az adaptív szabályozás néhány válfajával ismerkedünk meg.

Általában a tervezési cél az, hogy olyan szabályozót válasszunk, amely lehetővé teszi, hogy a szabályozott szakasz - azaz a folyamat - kimenete kövesse a bemeneti referenciajel által előírt jelet. Az általános bemenőjelen és beavatkozó jelen kívül vannak speciális bemenőjelek is, a zavarok. Ezeket nem mi szabályozzuk, mégis befolyásolják a kimenet viselkedését. Ezért a szabályozót úgy kell megtervezni - az előzőek figyelembevétele mellett -, hogy a zavaró hatások a szabályozott szakasz kimenetén már kompenzálódjanak. Tehát a két fő tervezési cél: a pályakövetés és a zavarkompenzáció megvalósítása. Ez minden szabályozási módszernek a központi kérdése [6].

A szabályozásnak eleget kell tennie a szabályozni kívánt műszaki folyamattal szemben támasztott minőségi követelményeknek. A minőségi követelmények egyrészt a szabályozás statikus pontosságát, azaz állandósult hibáját, másrészt dinamikus viselkedését, azaz szabályozási idejét, túllendülését írják elő. A valóságos és az előírt minőségi jellemzők összehasonlítása a szabályozási rendszer dinamikus viselkedésének vizsgálata alapján végezhető el.

A minőségi követelményeket egy modell segítségével is megfogalmazható, vagyis egy modell segítségével adható meg, hogy különböző alapjelre milyen válasz kívánatos a visszacsatolt rendszertől. Ha a szabályozott szakasz paraméterei állandóak és azokat pontosan ismerjük, akkor pontosan meghatározható, hogy milyen kompenzáló tagra van szükség a megkívánt viselkedés eléréséhez (feltéve, hogy nem támasztunk megvalósíthatatlan követelményeket a rendszerrel szemben). A gondolatsort folytatva eljutunk a modellreferenciás adaptív szabályozáshoz (a későbbiekben részletesen tárgyaljuk). A modellreferenciás szabályozóknál létezik egy szokásos visszacsatolt kört egy kompenzáló taggal. A visszacsatolt szakasz viselkedése egy referenciamodell segítségével definiálható. A modell és a visszacsatolt szakasz ugyanazt az alapjelet kapja meg.

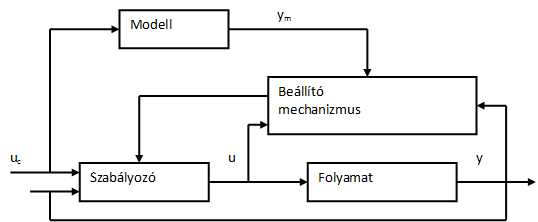
A modell és a visszacsatolt szakasz kimenő jelét összehasonlítjuk, és a kompenzáló tag paramétereit úgy változtatjuk meg, hogy a folyamat kimenőjele minden esetben a referenciamodell kimenőjeléhez közelítsen. Azzal a kikötéssel, hogy stabilis rendszert kapjunk. A modellreferenciás adaptív szabályozás alapstruktúrája 5-1. ábran látható. A modellreferenciás adaptív szabályozási sémát direkt módszereknek nevezzük, hiszen a beállító szabályok közvetlenül adják meg a kompenzáló tag megfelelő paramétereinek értékét.

5.1. ábra - Modell referenciás adaptív szabályozó

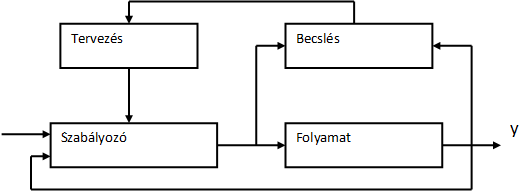
Másodikként az ún. self-tuning vagy önbeállító adaptív szabályozást kell megemlíteni. Ebben a sémában a szabályozott szakasz paramétereit folyamatosan megbecsüljük, a becsült paraméterek ismeretében folyamatosan újra tervezzük kompenzáló tag paramétereinek értékét. A self-tuning adaptív szabályozás alapstruktúrája a 5-2. ábran látható. A self-tuning szabályozási rendszer két hurkot tartalmaz. A belső hurok a folyamatból és egy közönséges lineáris visszacsatolásból áll. A szabályozási paraméterek a külső hurok által szabályozzuk, amely egy rekurzív paraméterbecslőből és egy ún. tervezőből áll. Sokféle self-tuning szabályozási sémát kaphatunk a különböző tervezési és becslési algoritmusok kombinálásával. A szabályozás további fontos tulajdonságai és példákon való alkalmazásának bemutatása a [1] irodalomban található.

Harmadikként a sztochasztikus adaptív szabályozásról szólunk tömören. A self-tuning szabályozásnál a kompenzáló tag paramétereinek tervezésekor a szabályozott szakasz becsült paramétereit már pontosnak tekintjük, nem vessztük számításba a becslés esetleges pontatlanságát. A sztochasztikus adaptív szabályozás ebben a tekintetben jelent továbblépést, a szabályozott szakasz paramétereit nem egy konkrét értékkel adjuk meg, hanem leképezzük a valószínűségi térbe, és itt vizsgáljuk a valószínűségi eloszlásukat, és ennek megfelelően avatkozhatunk be a szabályozási körbe. A sztochasztikus adaptív szabályozás részletes bemutatása a [1] irodalomban található.

5.2. ábra - Self-tuning szabályozási rendszer

Az adaptív rendszerek nemlineárisak. A viselkedésük egészen összetett és ez igen nehézzé teszi az analízisüket. Az elmélet lassan fejlődött és sok munkába került, míg-egy meglehetősen teljes és összefüggő elmélet jött létre. Természetesen ez az elmélet azért ma sem lezárt. Az adaptív rendszereket komplex viselkedésük következtében különböző szempontokból szükséges figyelembe venni. A nemlineáris rendszerek elmélete, a stabilitás, a rendszer identifikáció, a rekurzív paraméterbecslés, az optimális szabályozás és a sztochasztikus szabályozás mind hozzájárulnak az adaptív rendszerek megértéséhez.

Az adaptív rendszerek elméletének sokféle célja van. Elvárható, sőt szükséges, hogy olyan eszközök álljanak a rendelkezésünkre, amelyekkel egy adott rendszert tervezési szempontból elemezni tudunk. Egy tipikusnak tekinthető problémamegfogalmazás: olyan paraméter beállítási szabályt kell alkotni, amely gondoskodik a kívánt eredményekről egy stabil, zárthurkú rendszerben.

Szokás szétválasztani a beállás és az adaptáció problémáját. A beállás problémájánál azt feltételezzük, hogy a folyamat szabályozásánál vannak konstans, de ismeretlen paraméterek. Az adaptáció problémájánál viszont azt feltételezzük, hogy a paraméterek változnak. Néhány kérdést könnyebb a beállás problémájával kapcsolatban kezelni. Így például a paraméter konvergencia kérdését is, ahol azt kell meghatározni, hogy a paraméter konvergál-e a valódi értékéhez. Ez a probléma azonban tovább bonyolódik, ha a tényleges paraméterértékek is változnak. Hasonló becslési algoritmus használható beállásra és adaptációra.

Az adaptív szabályozás alapvető kérdése még a stabilitás. Ennek elemzésére sok erőfeszítés történt. Például a modellreferenciás adaptív szabályozás alapgondolata a stabilitás elméletéből ered. De a többi adaptív szabályozásnak is döntő kérdése ez.

5.3. A modellreferenciás adaptív szabalyozás

A változó paraméter és/vagy nemlinearitást tartalmazó folyamatok irányítása klasszikus eszközökkel általában nehézségekbe ütközik. A hirtelen zavarások időnként hatnak a folyamat jellemzőire. Ezek kompenzálása megoldható adaptív irányítási rendszerek alkalmazásával. Számos különböző adaptív irányítási rendszert javasoltak az utóbbi időben. [1] A jelen fejezetben kiemeljük a modellreferenciás adaptív rendszereket, mint az egyik legígéretesebb irányt.

A modellreferenciás adaptív rendszerek különleges típusú, általában nemlineáris szabályozási rendszerek. Tervezésük és alkalmazásuk szoros kapcsolatban áll a számítástechnikai eszközökkel, célszerűen mikroprocesszoros változatban történhet.

A további részekben megpróbáljuk részletesen is megvilágítani e szabályozások lényeges vonásait, továbbá megpróbáljuk bemutatni a működésüket, viselkedésüket, valamint létrejöttük hátterét. Szó lesz még a főbb kapcsolódó problémákról, ezek megoldásáról, valamint utoljára néhány alkalmazási példáról, s az ezekből levonható tapasztalatokról.

5.3.1. A modellreferenciás adaptív szabályozás alapjai

A modellreferenciás adaptív rendszerek alkalmazásának gondolata egy gyakorlati feladat megvalósítása során vetődött fel. A mai napig számos rendszert valósítottak meg és ezek működése fényesen igazolta a várakozásokat.

A modellreferenciás adaptív szabályozás alapstruktúrája a 5-1. ábran látható, amely jól mutatja, hogy a folyamat megkívánt működését egy referencia modell segítségével írtuk elő. A referencia modell meghatározza az alapjelre adandó ideális választ. A rendszer még tartalmaz egy közönséges visszacsatoló hurkot is, amely a folyamatból és a szabályozó egységből épül fel. A rendszer kimenete és a referenciamodell kimenőjele közötti különbség az " $e_{y} (t)$ " hiba

$e_{y} (t) = y (t) - y_{m} (t)$

(5.1)

A szabályozási paramétereket az e váltózásából számítjuk.

Így tehát egy modellreferenciás adaptív rendszerben két hurkot találhatunk: van egy belső hurok, amely egy közönséges szabályozási visszacsatolás és amely a folyamatot, valamint a szabályozó készüléket foglalja magába és van egy külső hurok, amely a belső hurokban a paraméterek beállítását végzi. Ez utóbbi úgy működik, azaz a paraméterek beállítása oly módon történik, hogy a folyamat " $y$ " kimenete és a modell " $y_{m}$ " kimenete között fellépő "e" hiba kicsi legyen. A belső hurok működése sokkal gyorsabb, mint a külsőé. A modellreferenciás adaptív szabályozás kulcsproblémája: úgy szabályozni a beállító mechanizmust, hogy stabil rendszert kapjunk, azaz az "e" hiba közelítsen a zérushoz.

Az eredeti modellreferenciás rendszert, - mint amilyen a 5-1. ábran is látható - Whitaker tervezte 1958-ban. E rendszer megalkotása két új gondolattal ismertette meg a szakembereket. Az első gondolat az volt, hogy a rendszer működését egy modell segítségével írta elő, a második gondolat pedig az volt, hogy a szabályozási paramétereket a referenciamodell és a rendszer kimenőjele közötti hiba alapján állította be. A modellreferenciás adaptív rendszerek eredetileg a determinisztikus, folyamatos idejű rendszerekben vizsgált szervo problémákból erednek. A gondolatot és az elméletet is később kiterjesztették a diszkrét idejű rendszerekre, valamint a sztochasztikus zavarokkal rendelkező rendszerekre is. E munkában azonban a szabályozás alapgondolatát helyeztük középpontba és a vizsgálatoknál, illetve az ismertetésnél is elsősorban a 5-1. ábran látható eredeti modellreferenciás adaptív rendszerre helyeztük a hangsúlyt. Ezt a rendszert szokás még ún. analóg modellreferenciás adaptív rendszernek is nevezni.

A szakirodalomban lényegében két fő megközelítése létezik a modellreferenciás adaptív rendszerek tervezésének és analízisének:

Gradiens módszer
Ljapunov módszer

A gradiens módszert Whitaker használta először, amikor az eredeti modellreferenciás adaptív rendszerekkel dolgozott. Ez a megközelítés azon a feltételezésen alapul, hogy a rendszer kiválasztott állapotváltozói - a paraméterek - sokkal lassabban változnak, mint a rendszer többi állapotváltozója. Ez a feltételezés, - amely megengedi a kvázi-stacionárius tárgyalást - lényegében az adaptációs eljáráshoz szükséges ún. érzékenységi deriváltak kiszámításában játszik fontos szerepet. A gradiens módszer nem fog szükségszerűen stabil eredményhez vezetni zárthurkú rendszerekben. Ez a megfigyelés ösztönözte a stabilitási elméletek felhasználását. A Ljapunov-féle stabilitási elméletet az adaptációs mechanizmus módosítására használták fel. A fentieken kívül még a modellkövetés is fontos része a modellreferenciás adaptív szabályozásnak, hasonlóan más adaptív szabályozásokhoz. A két fő megközelítésről még lesz szó, most a modellkövetés problémáját elemezzük röviden.

Ha egy beállítandó paraméterekkel rendelkező rendszerre a modellreferenciás adaptív szabályozást alkalmazzuk, akkor a paraméterek beállítására egy olyan módszert kapunk, ahol a zárt szabályozási hurok átviteli függvénye egy előírt modellhez fog közelíteni. Ezt hívják az ún. modellkövetés problémájának. Nagyon fontos kérdés, hogy milyen kicsire tudjuk csökkenteni az "e" hibát. Ez függ a modelltől, a rendszertől és az alapjeltől. Ha meg lehetne tenni azt, hogy a hiba minden alapjel esetén zérussal lesz egyenlő, akkor a legjobb modellkövetés valósul meg. A modellkövetés problémáját az ún. pólushely tervezést felhasználva tudjuk megoldani [11].

Egy szervo szabályozási probléma megfogalmazásának és megoldásának egy egyszerű és használatos módja a modellkövetés. Az alapgondolat nagyon egyszerű. A szervo működése közvetve van megadva úgy, hogy a kívánt rendszerválaszhoz egy matematikai modellt állítunk fel. Ez a modell lehet lineáris vagy nemlineáris. A paraméterek beállítása úgy történik, hogy a bemenőjelek egy adott osztályára, típusára nézve az " $y$ " kimenőjel a lehető legközelebb legyen az " $y_{m}$ " modell kimenőjelhez. Így látható, hogy a modellreferenciás adaptív rendszerekben az optimalizációs módszerek elengedhetetlenül fontos, de ugyanakkor természetes módszerek.

5.3.2. A gradiens módszer

Ebben a részben a modellreferenciás adaptív szabályozásoknál alkalmazott gradiens módszert mutatjuk be. Ez tulajdonképpen az egyik alapgondolata a modellreferenciás adaptív rendszerek megközelítésének, s egy megfelelő eljárás a paraméterek beállítására.

Feltételezzük, hogy a szabályozó paramétereit úgy szándékozzuk megváltoztatni, hogy a folyamat kimenete és a referencia modell kimenete között fellépő hiba a zérushoz tartson. Jelöljük a kimenőjel hibát " $e_{y} (t)$ "-vel, a rendszer paramétereit pedig " $θ$ "-val. Bevezetjük a következő kritériumfüggvényt:

$J (θ (t)) = \frac{1}{2} e_{y} {(t)}^{2}$

(5.2)

Ha a paramétereket a " $J (θ (t))$ " negatív gradiense irányában változtatjuk meg, akkor " $J (θ (t))$ " a még elfogadható legkisebb értékre állítható be:

$\frac{d θ (t)}{d t} = - γ \frac{\partial J (θ (t))}{\partial θ (t)} = - γ \frac{\partial e_{y} (t)}{\partial θ (t)} e_{y} (t)$

(5.3)

Ha feltételezzük azt, hogy a paraméterek sokkal lassabban változnak, mint a rendszer más állapotváltozói, akkor a, $\frac{\partial e_{y} (t)}{\partial θ (t)}$ deriválást azzal a feltételezéssel tehetjük, hogy a $θ (t)$ konstans. A $\frac{\partial e_{y} (t)}{\partial θ (t)}$ deriváltat a rendszer érzékenységi deriváltjának nevezzük. A (5.3) egyenletben felirt beállítási szabályt adaptációs törvénynek nevezik. A "" tényező az ún. adaptációs paraméter.

A (5.2) egyenletben bevezetett kritériumfüggvény természetesen tetszőleges. Megemlítjük a legegyszerűbb adaptációs törvényt is, ahol semmi mást nem veszünk figyelembe, csak azt, hogy milyen irányú, azaz milyen előjelű a változás. Ennek alakja a következő:

$\frac{d θ (t)}{d t} = - γ sign (\frac{\partial e_{y} (t)}{\partial θ (t)}) sign (e_{y} (t))$

(5.4)

Visszatérve a (5.3) adaptációs törvényhez, a kompenzáló tagban több beállítandó paraméter található, akkor a " $θ (t)$ " változó hetére egy oszlopvektort kell helyettesíteni, a $\frac{d θ (t)}{d t}$ derivált pedig a hiba gradiense a paraméterekre vonatkozóan.

A gradiens módszer néhány fontos tulajdonsága:

Nem szükséges a legjobb modellkövetést megkívánni. Az eljárás nemlineáris rendszereknél is felhasználható, valamint csak részben ismert rendszerek kezelésére is alkalmas.
Bizonyos közelítések szükségesek a tényleges paraméterbeállítási törvények, azaz az adaptációs törvények meghatározásához.
A $θ (t)$ paraméter konvergenciája leáll, ha $e_{y} (t) = 0$ Ekkor nincs megfelelő gerjesztés

Az adaptációs törvény megfelelően működik, ha a adaptációs paraméter kicsi. A megengedhető mértéke függ az alapjel nagyságától, valamint a folyamat körerősítésétől. Következésképpen nem adhatóak meg állandó határok rá, amivel a stabilitást garantálhatnánk. Az adaptációs törvény ekkor instabil zárthurkú rendszert eredményez.

5.3.3. A Ljapunov-módszer

Látható volt az előző részben, hogy a gradiens módszer önmagában nem ad megfelelő biztosítékot arra, hogy stabilis rendszert kapjunk, illetve arra, hogy a paraméterek a megfelelő paraméterekhez tartsanak. Mindez csak megfelelő gerjesztés esetén valósul meg, ha ez nem így van, a konvergencia azonnal leáll. Tehát a konvergencia alapjelfüggő, azaz fontos a gerjesztés szerepe.

Mi azonban szeretnénk egy olyan módszert, amely minden esetben stabilis rendszert eredményez és a paraméterek a megfelelő paraméterekhez tartanak. Azt tudjuk, hogy az $e_{y} (t) = 0$ állapotot szeretnénk stabilis állapotnak, ezért olyan törvényre van szükség, amely a rendszert ez irányba viszi. A legalkalmasabb ötletnek a Ljapunov-féle stabilitás tűnik, amely nemlineáris rendszerek esetén is alkalmazható. E szerint egy rendszer stabilis, ha egy alkalmasan választott ún. Ljapunov-függvénye pozitív definit, míg e függvény idő szerinti első deriváltja negatív definit.

A szabályozási paraméterek beállítására egyszerű törvények kaphatóak, amelyek a Ljapunov-függvényből származnak. Ezek az adaptációs törvények, hasonlóan a gradiens módszernél megismertekhez. Az ily módon kapott törvények mindig stabilis rendszerhez vezetnek. Egyetlen nehézség a Ljapunov- függvény megválasztása, de ez a módszer egyszerűsége miatt hamar kamatozódik. A gradiens módszerről és a Ljapunov-módszerről további részleteket a [1] irodalomban olvashatunk.

5.4. Kidolgozott feladat a modell referenciás adaptív szabályozókkal kapcsolatban

5 . 1 feladat Egy- energiatárolós rendszer modell referenciás adaptív szabályozása (gradiens módszer)

Tegyük fel, hogy a szabályozott szakasz egyenergiatárolós, és a következő differenciálegyenlettel irható le.

$\frac{d y (t)}{d t} = - a y (t) + b u (t)$

(5.5)

ahol $u (t)$ a beavatkozó jel és $y (t)$ a folyamat kimenő jele. Feltételezzük továbbá azt, hogy $a$ és $b$ paraméter nem ismert. Szabályozással az a célunk, hogy a visszacsatolt rendszer a következő differenciál egyenlet szerint viselkedjen

$\frac{d y_{m} (t)}{d t} = - a_{m} y_{m} (t) + b_{m} u_{r} (t)$

(5.6)

ahol $a_{m}$ és $b_{m}$ a referencia modell paraméterei és $u_{r} (t)$ a visszacsatolt rendszer alapjele.

A folyamat és a modell paramétereit a következő módon választottuk.

$a = 10$ $b = 5$ $a_{m} = 20$ $b_{m} = 20$

(5.7)

A MatLab kód

a=10;
b=5;
am=20;
bm=20;
g=100;
ampl=10;
fr=1;

E paraméterekkel az eredeti rendszer és a modell időállandója, valamint erősítése

$T = 0.1$ $G = 5$ $T_{m} = 0.05$ $G_{m} = 1$ 0

(5.8)

Látható, hogy a modell kétszer olyan gyors, mint az eredeti rendszer, és az erősítése is kétszerese az eredeti rendszer erősítésének.

Megoldás

Először azt feltételezzük, hogy a szabályozó paraméterei konstansak. Válasszuk a következő szabályozási törvényt

$u (t) = R u_{r} (t) - P y (t)$

(5.9)

Ha pontosan ismernénk a folyamat $a$ és $b$ paraméterét, akkor $R$ és $P$ konstans pontosan meghatározható lenne. Az (5.6) és (5.9) egyenletet összevetve

$R = \frac{b_{m}}{b}$

(5.10)

$P = \frac{a_{m} - a}{b}$

(5.11)

Alkalmazzuk először a gradiens. módszert! Először az e hibát kell kifejezni az $R$ és $P$ paraméterek függvényében.

$e_{y} (t) = y (t) - y_{m} (t)$

(5.12)

A (5.5) és (5.9) egyenletek Laplace transzformálva

$Y (s) = \frac{b R}{s + a + b P} U_{r} (s)$

(5.13)

Az érzékenységi deriváltak (5.13)-ből kifejezhetőek.

$\frac{\partial e_{y} (s)}{\partial R} = \frac{b}{s + a + b P} U_{r} (s)$

(5.14)

$\frac{\partial e_{y} (s)}{\partial P} = \frac{- b^{2}}{{(s + a + b P)}^{2}} U_{a} (s) = \frac{b}{s + a + b P} Y (s)$

(5.15)

Sem az $a$ és $b$ modell paraméter, sem a szabályozó $R$ és $P$ paramétere nem ismert. Innen meg kell engednünk az $R$ és $P$ paraméter lassú változását így azokat jelöljük $r (t)$ és $p (t)$ időfüggvénnyel. Ha ezek Laplace-transzformáltját behelyettesítjük (5.14) és (5.15) egyenletekbe, akkor olyan összefüggést kapunk, amelyet közvetlenül nem tudunk használni. Közelítéssel kell élnünk. Ha a szabályozási paraméterek közelítenek az ideálishoz, akkor igaz a következő

$s + a + b P (s) \approx s + a_{m}$

(5.16)

Szükségünk van az adaptáció mértékét (gyorsaságát) megadó paraméterre. Látható ez paraméter összevonható $b$ paraméterrel. Visszatérve az időtartományban. Ennek megfelelően az adaptációs algoritmus a következő

$\frac{d r (t)}{d t} = - γ ℒ^{- 1} (\frac{1}{s + a_{m}} U_{r} (s)) e_{y} (t)$

(5.17)

$\frac{d p (t)}{d t} = γ ℒ^{- 1} (\frac{1}{s + a_{m}} Y (s)) e_{y} (t)$

(5.18)

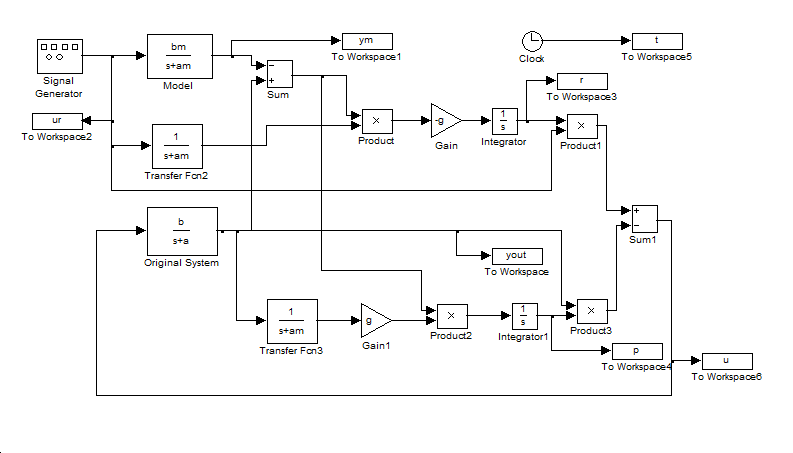
(5.17) és (5.18) úgy értelmezhető, hogy a referemcia jelet és a kimenőjelet átvezetjük egy

$W (s) = \frac{1}{s + a_{m}}$

(5.19)

átviteli függvénnyel rendelkező tagon, majd az eredményt összeszorozzuk a kimenőjel hibájával. E szorzatot a megfelelő előjelű adaptációs paraméterrel megszorozva és integrálva kapjuk meg a szabályozó két paraméterét. (a MATLAB programban az adaptációs paramétert $g$ jelöli)

5.3. ábra - Adaptív szabályozás gradiens módszerrel

Az ideális szabályozási paraméterek

$R = 4 P = 2$

(5.20)

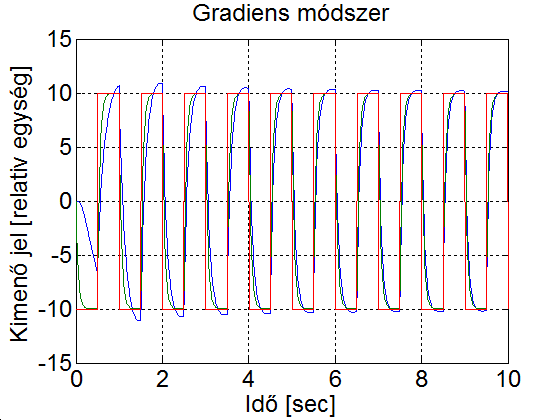
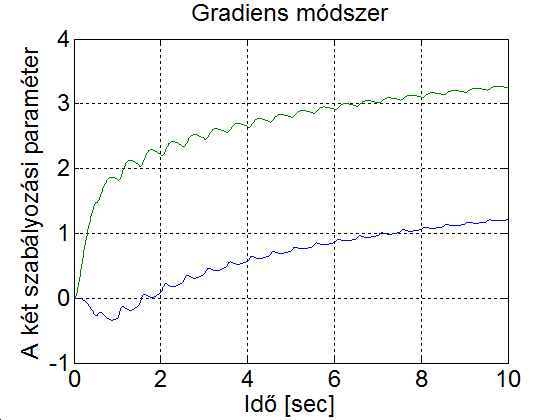
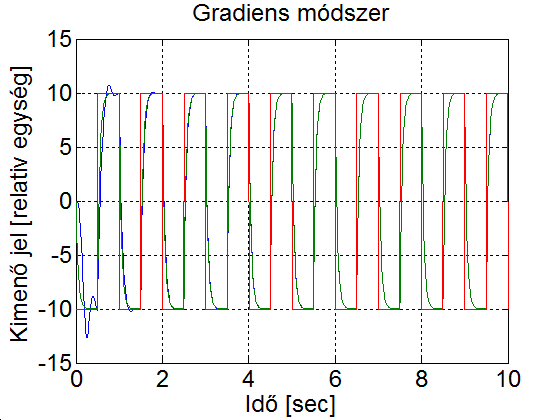
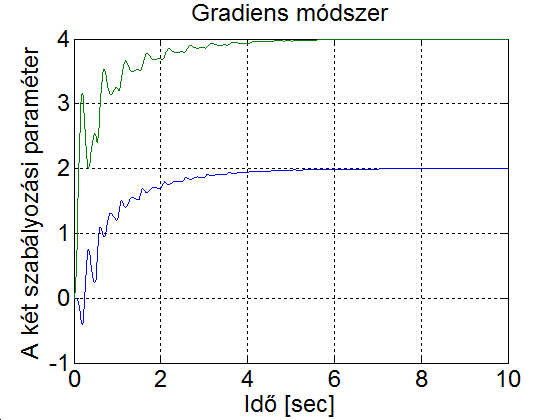
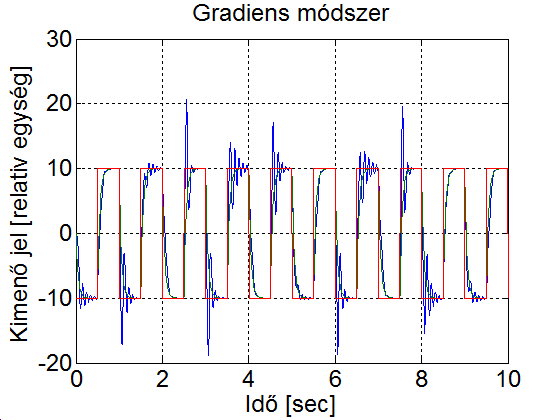
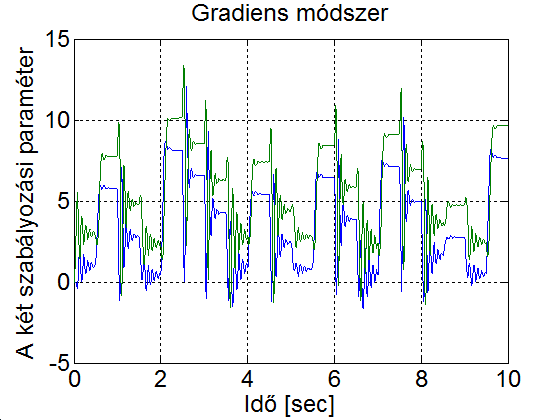
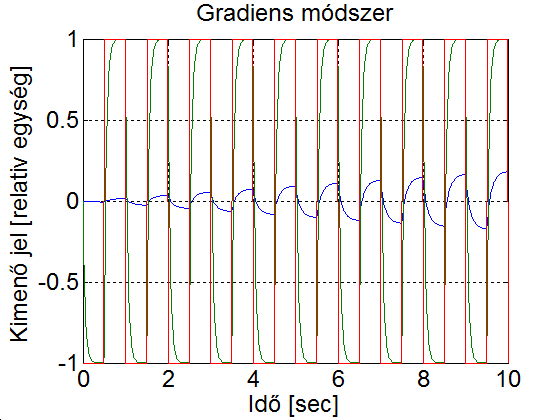
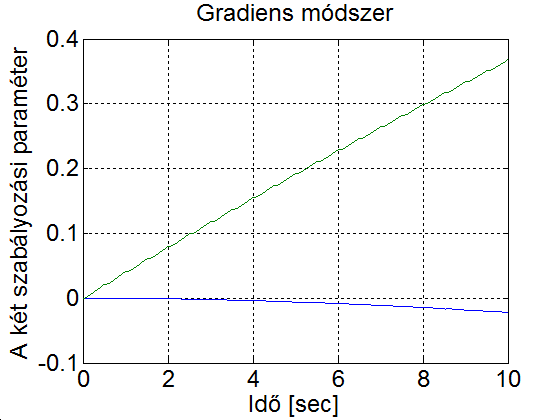
Legyen az $u_{r}$ egy 1 amplitúdójú 1 Hz frekvenciájú négyszögjel és az adaptációs paraméter legyen 1. A szimulációs eredmény a 5-4. ábran látható. Mefigyaelhető, hogy az első néhány periódusban a modell (zöld) és a visszacsatolt rendszer (kék) viselkedése jelentősen eltér. Majd ahogy a szabályozási paraméterek közelítenek az ideális értékekhez, a modell (zöld) és a visszacsatolt rendszer (kék) görbéje közelít egymáshoz. Ha megnözeljük az adaptációs paraméter értékét a 10-szeresére, ekkor a szabályozási paraméterek jelentős lengések után az előző esetnél gyorsabban elérik el az ideális értéket (ld. 5-5. ábra). Ha a tanulási paramétert túl nagyra választjuk, akkor az a rendszer instabilitását jelentheti (ld. 5-6. ábra). Az is könnyen belátható, hogy a modell referenciás adaptív szabályozás nem lineáris, vagyis a szuperpozíció elve nem érvényes rá. Ehhez elegendő azt bemutatni, ha az $u_{r}$ referencia jelet tizedére csökkentjük, akkor a választ nem kapjuk meg egyszerűen annak tizedésre csökkentésével. Az $u_{r}$ referencia jel csökkentésével a válasz jellege is megváltozik, mert a szabályozási paraméterek lassabban konvergálnak az ideális értékhez. (ld. 5-7. ábra)

A nyomtatáshoz használt MATLAB kód

plot(t,yout,t,ym,t,ur)
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('Kimenő jel [relativ egység]');
title('Gradiens módszer');
% you can adjust your axis
%axis([0 1 -10 10]);
grid
pause
 
plot(t,p,t,r)
set(gca, 'fontsize', [18]);
xlabel('Idő [sec]');
ylabel('A két szabályozási paraméter');
title('Gradiens módszer');
% you can adjust your axis
%axis([0 1 0 5]);
grid

5.4. ábra - Szimulációs eredmény ()

5.5. ábra - Szimulációs eredmény ()

5.6. ábra - Szimulációs eredmény ()

5.7. ábra - Szimulációs eredmény ()

5 . 2 feladat Egy-energiatárolós rendszer modell referenciás adaptív szabályozása (Lajpunov módszer)

Oldjuk meg az előző feladatot a Ljapunov stabilitási kritériumon alapuló adaptációs törvényt alkalmazva.

Megoldás

Egy olyan Lyapunov függvényre van szükség, ami az általunk elérni kívánt állapotban zérus értékű (ez lesz a nemlineáris rendszer stabilis állapota), minden más állapotban pozitív. A célunk az, hogy a kimenőjel $e_{y} (t)$ hibája nulla legyen, a szabályozási paraméterek egyezzenek meg az ideális (5.10) és (5.11) összefüggéssel megadott értékekkel. Ennek megfelelő Lyapunov függvény

$V (e_{y}, r, p) = \frac{1}{2} (e_{y} {(t)}^{2} + γ^{- 1} {(r - \frac{b_{m}}{b})}^{2} + γ^{- 1} {(p - \frac{a_{m} - a}{b})}^{2})$

(5.21)

Deriváljuk a $V (e_{y}, r, p)$ függvényt az idő szerint

$\frac{d V (e_{y}, r, p)}{d t} = e_{y} (t) \frac{d e_{y} (t)}{d t} + γ^{- 1} (r (t) - \frac{b_{m}}{b}) \frac{d r (t)}{d t} + γ^{- 1} (p (t) - \frac{a_{m} - a}{b}) \frac{d p (t)}{d t}$

(5.22)

Fejezzük ki az $e_{y} (t)$ hiba idő szerinti első deriváltját

$\frac{d e_{y} (t)}{d t} = a_{m} e_{y} (t) + (a_{m} - a - b p (t)) y (t) + (b r (t) - b_{m}) u_{r} (t)$

(5.23)

A (5.23) kifejezést (5.22)-ba helyettesítve

$\frac{d V (e_{y}, r, p)}{d t} = - a_{m} e_{y} {(t)}^{2} + γ^{- 1} (r (t) - \frac{b_{m}}{b}) (\frac{d r (t)}{d t} + γ u_{r} (t) e_{y} (t)) + γ^{- 1} (p (t) - \frac{a_{m} - a}{b}) (\frac{d p (t)}{d t} - γ y (t) e_{y} (t))$

(5.24)

Ljapunov stabilitási kritérium értelmében $\frac{d V (e_{y}, r, p)}{d t}$ függvénynek az általunk elérni kívánt állapoton kívül negatívnak kell lennie. A (5.24) kifejezés jobb oldalán az első tag nem lehet pozitív, ezért ha az adaptációs törvényt úgy választjuk, hogy a többi tag zérus értékű legyen, akkor egy olyan stabilis rendszert kapunk, ahol az $e_{y} (t)$ hiba zérushoz tart és a szabályozási paraméterek az ideális értékhez tartanak. Az adaptációs törvény

$\frac{d r (t)}{d t} = - γ u_{r} (t) e_{y} (t)$

(5.25)

$\frac{d p (t)}{d t} = γ y (t) e_{y} (t)$

(5.26)

Ha (5.17) és (5.18) adaptációs törvényeket összevetjük (5.25) és (5.26) adaptációs törvényekkel, akkor azt tapasztaljuk, hogy a gradiens módszer esetén $u_{r} (t)$ és $y (t)$ egy aluláteresztő szűrőn halad keresztül, mielőtt összeszoroznánk $e_{y} (t)$ hibajellel. Ezzel szemben a Lapunov módszer esetén ez az aluláteresztő szűrő hiányzik az $u_{r} (t)$ és $y (t)$ jeleket közvetlenül szorozzuk meg $e_{y} (t)$ hibajellel.

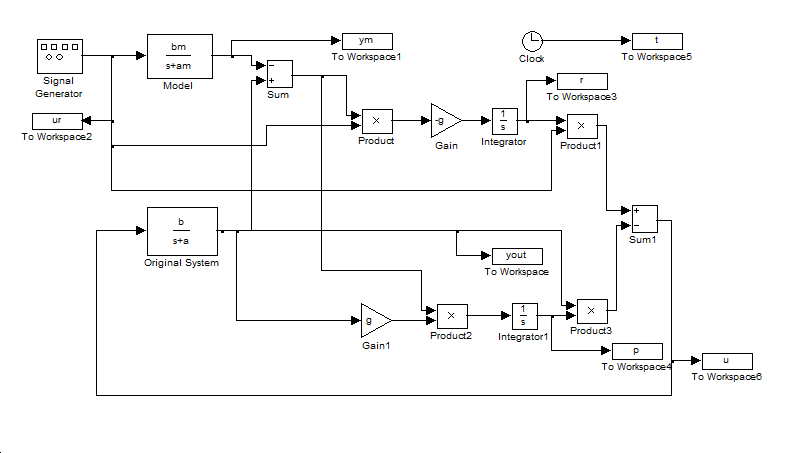
5.8. ábra - Adaptív szabályozás Ljapunov módszerrel

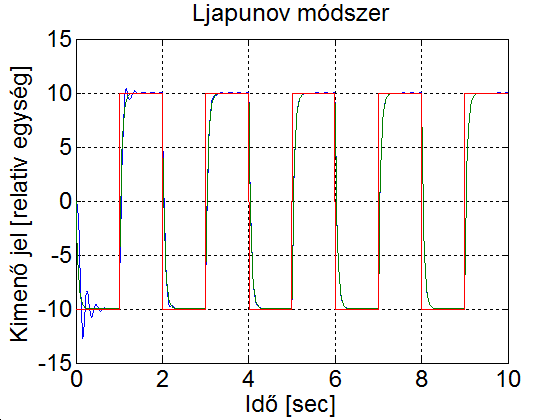
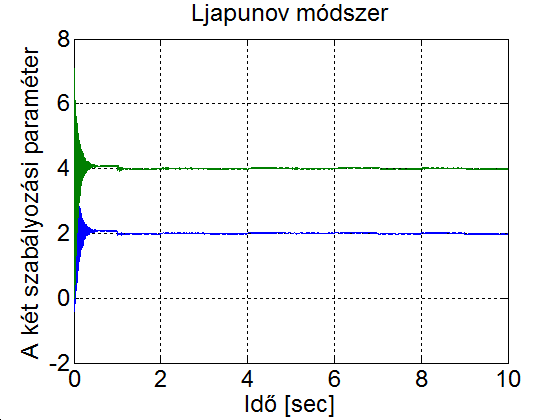
Ha 5-4. ábrat és 5-9. ábrat összevetjük, akkor megállapíthatjuk, hogy a Ljapunov módszerrel a szabályozási paraméterek gyorsabban konvergálnak az ideális értékhez, mint a gradiens módszerrel és kevésbé hajlamos az instabilitásra (ld. 5-6. ábra és 5-10. ábra)

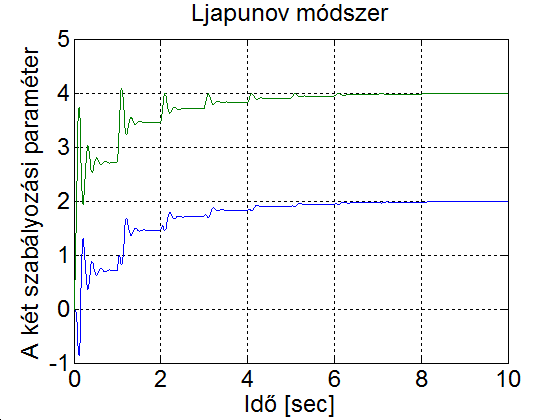
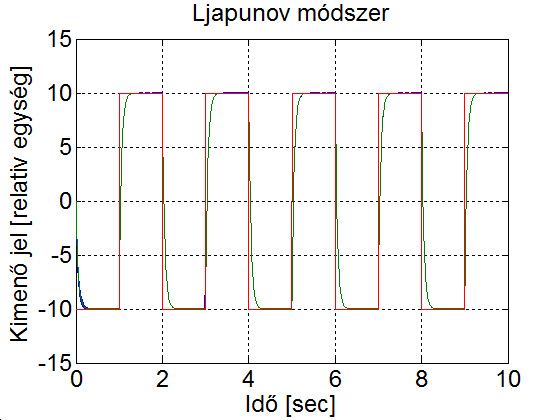
5.9. ábra - Szimulációs eredmény ()

5.10. ábra - Szimulációs eredmény ()

5 . 3 feladat Kéttagú robotkar modell referenciás adaptív szabályozása (Lajpunov módszer)

Feltéve, hogy az összes állapotváltozó mérve van, gyakran találunk olyan lineárisan változó hibát, amely megkönnyíti a stabil modellreferenciás adaptív irányítás megtervezését. Ez abban az esetben is magyarázatot ad a vezérlés hibájára, ha a dinamikai folyamat nemlineáris.

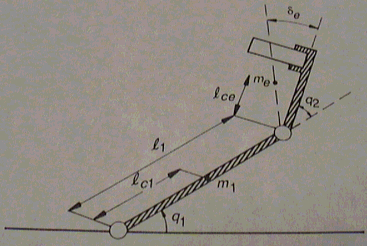
A módszert nézzük most meg egy példa segítségével, amelyben egy kéttagú robotkart fogunk vizsgálni (ld. 5-11. ábra). A második tagot az ismeretlen teherrel egy bővített tagként kezeljük, amely négy ismeretlen paraméterrel rendelkezik. Ezek a tömeg (me), az inercia (Ie), a tömegközéppont távolsága (le), valamint az eredeti taghoz képesti szögelfordulás (e).

5.11. ábra - Kéttagú robotkar ismeretlen terheléssel

Megoldás

A modellnek megfelelően a közvetlen hajtást a következőképpen írhatjuk le:

$H (q) \ddot{q} + C (q, \dot{q}) \dot{q} + G (q) = T$

(5.27)

ahol q az általános koordináta, H az inercia mátrix, C a csillapítás mátrixsza a G pedig a gravitációs tag.

A beavatkozó jel a nyomaték, amelyet például áramszabályozással lehet változtatni.

$\frac{1}{2} \frac{d}{d t} ({\dot{q}}^{T} H \dot{q}) = {\dot{q}}^{T} H (q) \ddot{q} + {\dot{q}}^{T} C (q, \dot{q}) \dot{q} + = {\dot{q}}^{T} (T - G)$

(5.28)

A fenti egyenletből kiolvasható, hogy a mozgási energia deriváltja azonos a betáplált erővel és a gravitációs nyomatékkal.

Folytatva a szerkezetet leíró egyenleteket:

$H = (\begin{matrix} θ_{1} + 2 θ_{3} \cos q_{2} + 2 θ_{4} \sin q_{2} & θ_{2} + θ_{3} \cos q_{2} + θ_{4} \sin q_{2} \\ θ_{2} + θ_{3} \cos q_{2} + θ_{4} \sin q_{2} & θ_{2} \end{matrix})$

(5.29)

$G = (\begin{matrix} θ_{3} Y_{1} + θ_{4} Y_{2} + (θ_{1} - θ_{2} + e_{1}) e_{2} \cos q_{1} \\ θ_{3} Y_{3} + θ_{4} Y_{4} \end{matrix})$

(5.30)

ahol

$Y_{1} = - 2 \sin (q_{2}) {\dot{q}}_{1} {\dot{q}}_{2} - \sin (q_{2}) {\dot{q}}_{2}^{2}$

$Y_{2} = 2 \cos (q_{2}) {\dot{q}}_{1} {\dot{q}}_{2} + \cos (q_{2}^{2})$

$Y_{3} = \sin (q_{2}) {\dot{q}}_{1}^{2} + e_{2} \cos (q_{1} + q_{2})$

$Y_{4} = - \cos (q_{2}) {\dot{q}}_{1}^{2} + e_{2} \sin (q_{1} + q_{2})$

$e_{1} = m_{1} l_{1} l_{c 1} - m_{1} l_{c 1}^{2}$

$e_{2} = g / l_{1}$

Itt g a normális gyorsulás, 1…4 pedig a négy fizikai paraméter függvényei:

$θ_{1} = I_{1} + m_{1} l_{c 1}^{2} + I_{e} + m_{e} l_{c e}^{2} + m_{e} l_{1}^{2}$

$θ_{2} = I_{1} + m_{e} l_{c e}^{2}$

$θ_{3} = m_{e} l_{1} l_{c e} \cos δ_{e}$

$θ_{4} = m_{e} l_{1} l_{c e} \sin δ_{e}$

A rendszer

$ϕ^{T} (q, \dot{q}, \ddot{q}) θ = T$

alakban írható fel, ahol T

$(\begin{matrix} {\ddot{q}}_{1} + e^{'} & {\ddot{q}}_{2} - e^{'} & 2 \cos (q_{2}) {\ddot{q}}_{1} + \cos (q_{2}) {\ddot{q}}_{2} + Y_{1} & 2 \sin (q_{2}) {\ddot{q}}_{1} + \sin (q_{2}) {\ddot{q}}_{2} + Y_{2} \\ 0 & {\ddot{q}}_{1} + {\ddot{q}}_{2} & \cos (q_{2}) {\ddot{q}}_{1} + Y_{3} & \sin (q_{2}) {\ddot{q}}_{1} + Y_{4} \end{matrix})$

(5.31)

alakban adható meg.

(5.32)

$T = (\begin{matrix} τ_{1} - e_{1} e_{2} \cos q_{1} \\ τ_{2} \end{matrix})$

(5.33)

Az előbbi példát általánosíthatjuk is. Ekkor felírhatjuk a rendszert leíró egyenletet:

$T - H^{'} (q) \ddot{q} - C^{'} (q, \dot{q}) \dot{q} - G^{'} (q) = ϕ^{T} (q, \dot{q}, \ddot{q}) θ^{0}$

(5.34)

amelyben H', C', G' és ismertek vagy mérhetők. Ha a modell nemlineáris, paraméterekben megadva lineárissá válik, amely változtatható. Nagyon fontos, hogy a folyamat során a kezdeti ismereteket használjuk fel, és hogy a rendszer nem tekinthető úgy, mint egy "fekete doboz" modell az idő szerint változó paraméterekkel. A modell nem lesz megfelelő, amíg nem mérjük a gyorsulás, a helyzet és a sebesség értékeit.

Legyen a referencia trajektória a pozíció (qm) és a sebesség ( ${\dot{q}}_{m}$ ). Ekkor felírhatjuk Lyapunov függvényét:

$V = \frac{1}{2} ({\dot{\tilde{q}}}^{T} H (q) \dot{\tilde{q}} + {\tilde{q}}^{T} K_{p} \tilde{q} + {\tilde{θ}}^{T} Γ \tilde{θ})$

(5.35)

ahol $\tilde{q} = q - q_{m}$ , $\dot{\tilde{q}} = \dot{q} - {\dot{q}}_{m}$ , $\tilde{θ} = θ - θ^{0}$ , valamint Kp és pozitív definitű mátrixok. Differenciálva V-t:

$\dot{V} = {\dot{\tilde{q}}}^{T} H \ddot{\tilde{q}} + \frac{1}{2} {\dot{\tilde{q}}}^{T} \dot{H} \dot{\tilde{q}} + {\dot{\tilde{q}}}^{T} K_{p} \tilde{q} + {\tilde{θ}}^{T} Γ \tilde{θ}$

$= {\dot{\tilde{q}}}^{T} (H \ddot{q} - H {\ddot{q}}_{m} + C \dot{\tilde{q}} + K_{p} \tilde{q}) + {\tilde{θ}}^{T} Γ \dot{\tilde{θ}}$

$= {\dot{\tilde{q}}}^{T} (T - G - H {\ddot{q}}_{m} + C {\dot{q}}_{m} + K_{p} \tilde{q}) + {\tilde{θ}}^{T} Γ \dot{\tilde{θ}}$

(5.36)

A kapott eredményre alkalmazva a szabályozási-, illetve az adaptációs törvényeket:

$T = H^{'} {\ddot{q}}_{m} + C^{'} {\dot{q}}_{m} + G^{'} - K_{p} \tilde{q} - K_{d} \dot{\tilde{q}}$

(5.37)

$\dot{V} = {\dot{\tilde{q}}}^{T} (\tilde{H} {\ddot{q}}_{m} - \tilde{C} {\dot{q}}_{m} + \tilde{G} - K_{d} \dot{\tilde{q}}) + {\tilde{θ}}^{T} Γ \dot{\tilde{θ}}$

(5.38)

ahol

$\tilde{H} (q) = H^{'} (q) - H (q)$

$\tilde{C} (q, \dot{q}) = C^{'} (q, \dot{q}) - C (q, \dot{q})$

$\tilde{G} (q) = G^{'} (q) - G (q)$

(5.39)

Bevezetjük a

$\tilde{H} {\ddot{q}}_{m} - \tilde{C} {\dot{q}}_{m} + \tilde{G} = ϕ_{m}^{T} \tilde{θ}$

(5.40)

egyenletet. Ezt azért tehetjük meg, mivel a paraméterek függvényében a modellünk is lineáris. Ezen kívül $ϕ_{m} = ϕ_{m} (q, \dot{q}, {\dot{q}}_{m}, {\ddot{q}}_{m})$ , ami azt jelenti, hogy csak a modell trajektóriájának gyorsulása ismert, nem pedig az eredeti gyorsulások. Így:

$\dot{V} = - {\dot{\tilde{q}}}^{T} K_{d} \dot{\tilde{q}} + {\tilde{θ}}^{T} (Γ \dot{\tilde{θ}} + ϕ_{m}^{T} \dot{\tilde{q}})$

(5.41)

amely a paraméterek megváltozását eredményezi:

$\dot{θ} = \dot{\tilde{θ}} = - Γ^{- 1} ϕ_{m}^{T} \dot{\tilde{q}} = - Γ^{- 1} ϕ_{m}^{T} (\dot{q} - {\dot{q}}_{m})$

(5.42)

a Ljupanov-függvény tulajdonságából következik, hogy ez egy pozitív definit, és hogy a derivált

$\dot{V} = - \dot{\tilde{q}} K_{d} \dot{\tilde{q}}$

(5.43)

negatív szemidefinit. Ez azt jelenti, hogy a zártláncú rendszer stabil, illetve az állandósult sebesség hibája zérus. A szabályozó segítségével a pozíciók hibái is zérusra csökkenthetők.

Vissza		Előre
4. fejezet - Feladatok a visszacsatolt rendszer stabilitásával kapcsolatban	Főoldal	6. fejezet - Állapottér reprezentáció