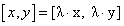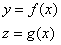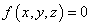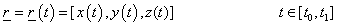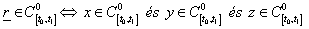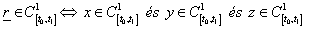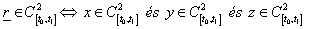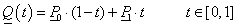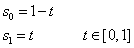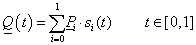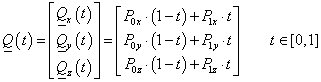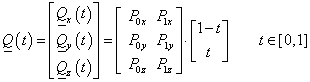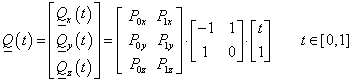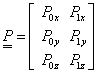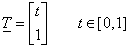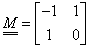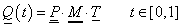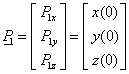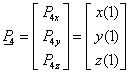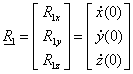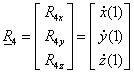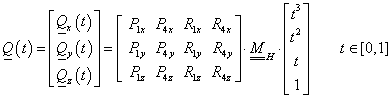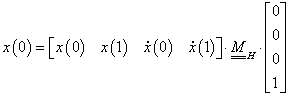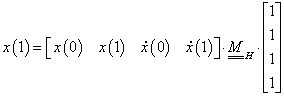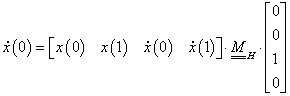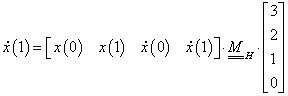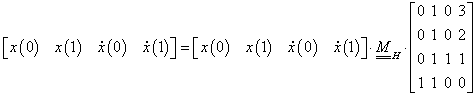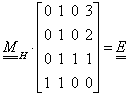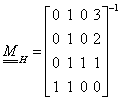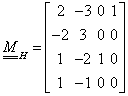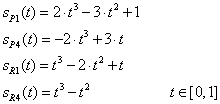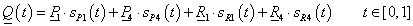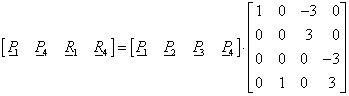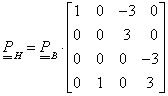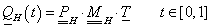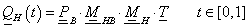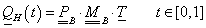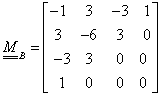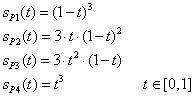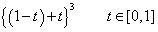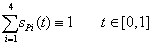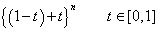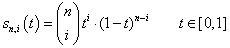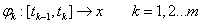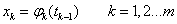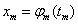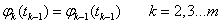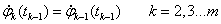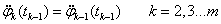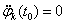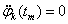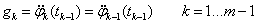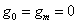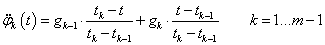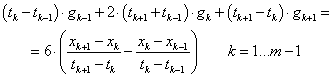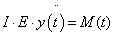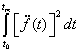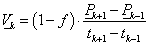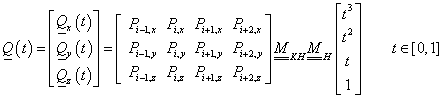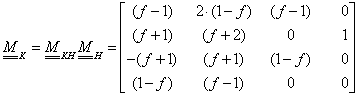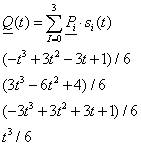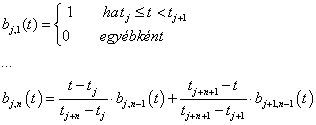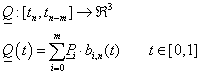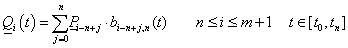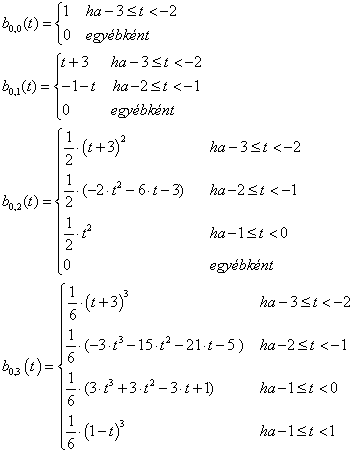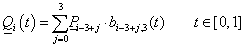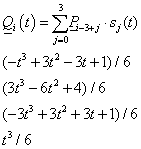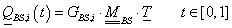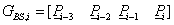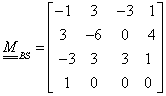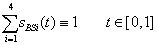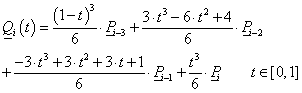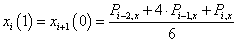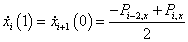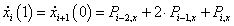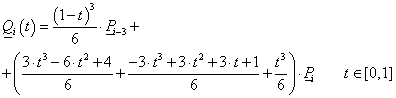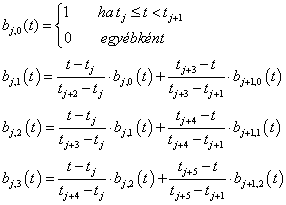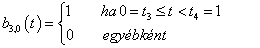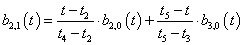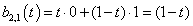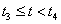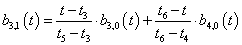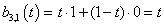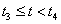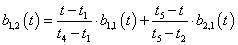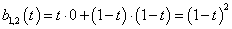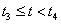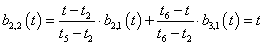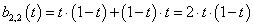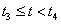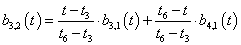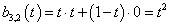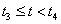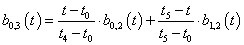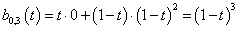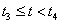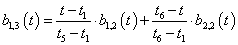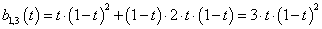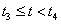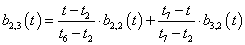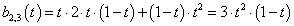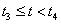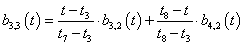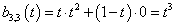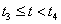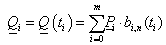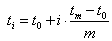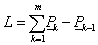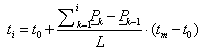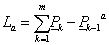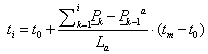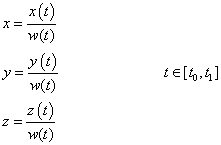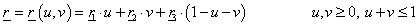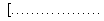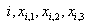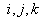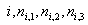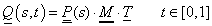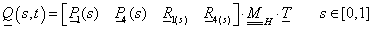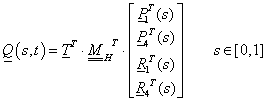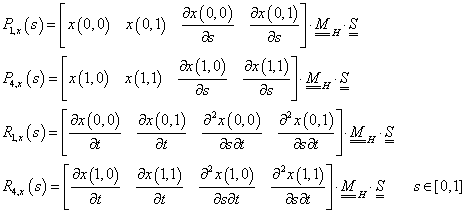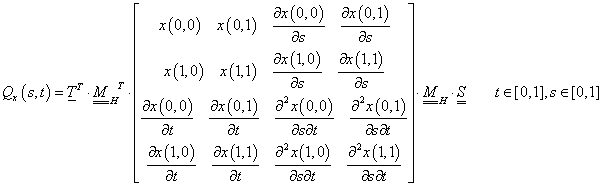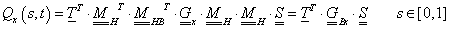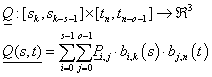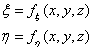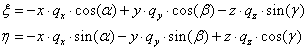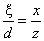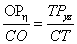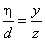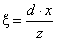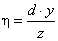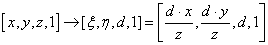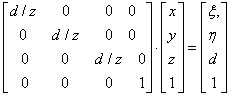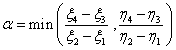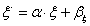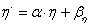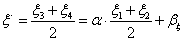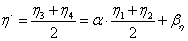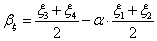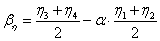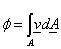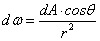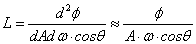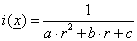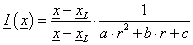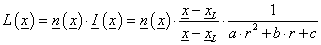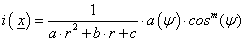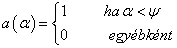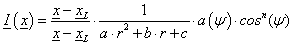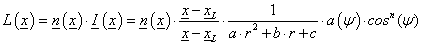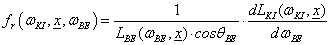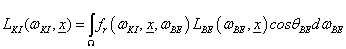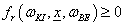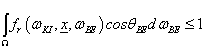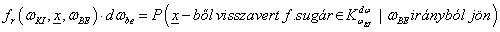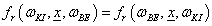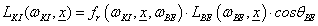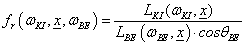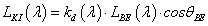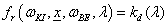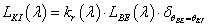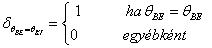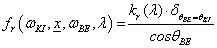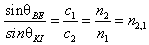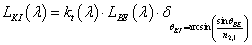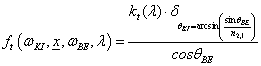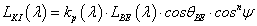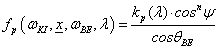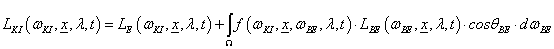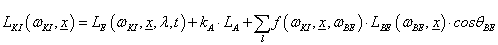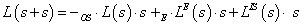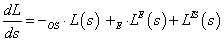3. fejezet - A 3D grafika elméleti alapjai
- 3.1. Grafikus tárgymodellek
- 3.2. Koordináta-rendszerek
- 3.3. Görbék, felületek és testek
-
- 3.3.1. Paraméteres görbemegadás
- 3.3.2. Folytonosság és geometriai folytonosság
- 3.3.3. Az elsőfokú paraméteres görbeszakasz leírása
- 3.3.4. Hermite-féle harmadfokú görbeszakasz
- 3.3.5. Bezier-féle harmadfokú görbeszakasz
- 3.3.6. Természetes spline
- 3.3.7. Catmull-Rom görbék, a kardinális spline
- 3.3.8. B-spline-ok
- 3.3.9. Szabadformájú felületek
- 3.3.10. Testek
- 3.4. A megjelenítő cső
- 3.5. A képszintézis alapfogalmai
- Irodalmak:
A 3D grafika témája a valóság objektumainak tárolása és megjelenítése.
3.1. Grafikus tárgymodellek
Az adatok tárolási stratégiája meghatározza a megjelenítést is.
3.1.1. Raszteres és vektoros leírás
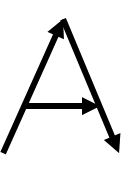
Grafika tárolására két alapvető stratégia létezik. Az egyik eset, amikor a kép olyan mintha ceruzával rajzolnánk. Ilyenkor a kép adatainak tárolása úgy történik, hogy tároljuk a kép rajzolásához szükséges vonaldarabok (vektorok) adatait, és ennek alapján megrajzolhatjuk a képet. Az ilyen tárolási módot vektoros képtárolásnak hívják. A 3.1. ábra egy nagy A rajzolatát mutatja vektorosan.
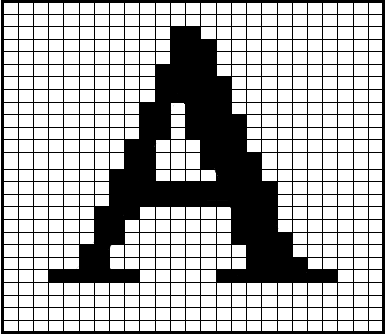
Lehetőségünk van arra is, hogy a képet képpontokra (raszterpontokra) osszuk és minden egyes pontról tároljuk annak színét. Ezt a raszteres képet a térképhez való hasonlatossága miatt bitképnek hívjuk. A 3.2. ábra egy ilyen fekete-fehér bitképét mutatja egy A betűnek.
3.2. Koordináta-rendszerek
A objektumok térbeli elhelyezkedésének megadásakor vonatkoztatási rendszerre, koordináta-rendszerre van szükségünk.
3.2.1. Leggyakrabbak használt koordinátarendszerek
Matematikai tanulmányainkból ismertek a Descartes féle derékszögű koordináta-rendszer, a henger és gömbi koordináta-rendszerek egyaránt.
3.2.2. Homogén koordináták
Az olyan koordináta-rendszereket nevezzük homogénnek, amelyekben a pontot azonosító, rendezett pár (hármas, négyes stb.) elemeit egy nullától különböző számmal megszorozva, ugyanazt, a pontot azonosító párt (hármast, négyest…) kapjuk [3.1.] .
|
|
Ha egy síkbeli pontot szeretnénk leírni, akkor azt megtehetjük úgy, hogy a síkot kiemeljük a térbe. A z=1 lesz a sík egyenlete, és a tér pontját az [x,y,1] homogén koordinátákkal megadott ponttal jellemezzük. Világos, hogy az azonos irányú [λ*x, λ*y, λ] ugyanaz a pontot jelöli ki a síkból (3.3. ábra)
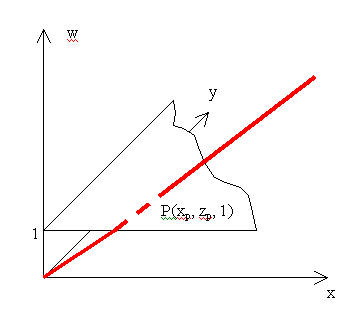
Hasonlóan járhatunk el térbeli koordináták esetén a negyedik koordináta (w=1) értéket választva a tér pontjait az [x,y,z,1] homogén koordinátás forma írja le.
A homogén koordináták igazi jelentőségét az adja, hogy használatukkal az ideális térelemek (pont, egyenes, sík) is megadhatók. Például, a 3.1. ábra esetén az [1,0,0] homogén koordinátákkal megadott pont az x irányú ideális pontját adja a síknak
3.3. Görbék, felületek és testek
A szabadformájú geometriai objektumok modellezéséhez foglalkoznunk kell a térgörbék és a térbeli felületek matematikai leírásával. Ezek használata megfelel a vektoros geometriai ábrázolásnak. Először a térgörbék leírását vizsgáljuk, majd ezt általánosítjuk a szabadformájú felületek leírására. A térgörbék közvetlen függvénnyel való leírása nem alkalmas tetszőleges görbe közelítő ábrázolására, mert nem tudjuk biztosítani koordinátákban megkövetelt egyértékűséget. A (3.1) közelítés esetében, amikor az x függvényében közelítjük az y és z koordinátákat, akkor nem fordulhat elő, hogy egyetlen x értékhez több (y,z) páros tartozzon, a görbe azonban visszatekeredhet oda.
|
|
(3.1) |
Az implicit görbemegadás, mely egy egyenlet gyökeinek görbéjét tartalmazza (3.2), gyakorlati szempontból használhatatlan.
|
|
(3.2) |
3.3.1. Paraméteres görbemegadás
A fenti megfontolások alapján a paraméteres görbemegadást használjuk. Ennek lényege, hogy egy, a koordinátáktól független paraméter-intervallumot választva, a t paraméter (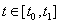 ) függvényeként írhatjuk fel a görbe pontjainak (x,y,z) koordinátáit (3.3).
) függvényeként írhatjuk fel a görbe pontjainak (x,y,z) koordinátáit (3.3).
|
|
(3.3) |
Gyakorlatilag tehát a térgörbét, mint egy vektor-skalár függvényt ábrázoljuk (3.4) [3.2.] .
|
|
(3.4) |
3.3.2. Folytonosság és geometriai folytonosság
Egy térgörbe akkor és csak akkor folytonos, ha koordinátafüggvényei folytonosak. Tehát
|
|
(3.5) |
Az intervallumon folytonos függvényeket C-vel jelöljük, a felső indexben 0-val (0. derivált folytonos), az alsó indexben az intervallummal.
Egy térgörbe akkor és csak akkor folytonosan differenciálható (a felső indexben az első deriváltat 1 jelöli), ha koordinátafüggvényei folytonosan differenciálhatók (3.6). Tehát
|
|
(3.6) |
Hasonlóan egy térgörbe akkor és csak akkor kétszer folytonosan differenciálható, ha a koordinátafüggvények kétszer folytonosan differenciálhatók (3.7).
|
|
(3.7) |
Definiáljuk a geometriai folytonosság fogalmát!
Definíció: Két csatlakozó görbeszakaszt a csatlakozó pontban k. rendben geometriailag folytonosnak mondunk – és
G
k
-val jelöljük – akkor és csak akkor, ha mindkét görbeszakasznak létezik olyan paraméterezése, hogy a görbék a pont két oldalán számított paraméter szerinti i. deriváltjai (ahol i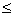 k) megegyeznek.
k) megegyeznek.
Ha a fenti definíciót a G 1 elsőrendű folytonosságra fogalmazzuk át, akkor a következő definíciót kapjuk.
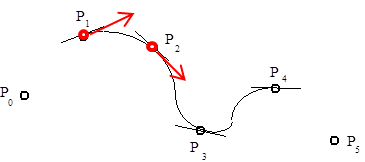
Definíció: Két folytonos (C 0 ) görbe akkor és csak akkor folytonos geometriailag 1. rendben (G 1 ), ha a csatlakozó pontban a két görbe érintővektora egy irányba mutat. Más szavakkal, ha f(u) és g(v) görbék csatlakoznak akkor a csatlakozási pontban f ’(u) és g ’(v) párhuzamosak, és skaláris szorzatuk nem negatív. (3.4. ábra)
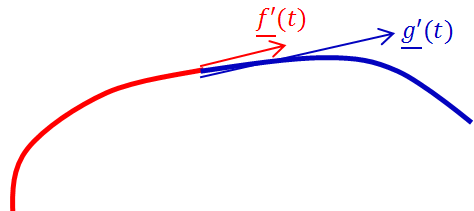
Érdemes megjegyezni, hogy elegendő csak az egyirányúságot kikötni, hiszen az egyik oldalon lineáris átparaméterezéssel a görbe „bejárásának” sebessége skálázható. A második megfogalmazásban a skaláris szorzatra való megkötés a párhuzamos, de ellenkező irányba mutató érintőket szűri ki.

A G2 másodrendű geometriai folytonosság meghatározására igaz a következő, G. Neilson nevéhez fűzhető tétel is:
Tétel: Két C
1
folytonosan csatlakozó görbeszegmens akkor és csak akkor csatlakozik G
2
folytonosan, ha a második derivált vektorok különbsége párhuzamos a közös érintővektorral, azaz 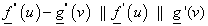 .
.
Nyilvánvaló, hogy k.-rendű geometriai folytonosságból nem következik a k.-rendű matematikai folytonosság, azaz 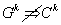 , hiszen például első rendben csak azt írtuk elő, hogy az érintők egy irányba mutatnak és nem azt, hogy egyenlők.
, hiszen például első rendben csak azt írtuk elő, hogy az érintők egy irányba mutatnak és nem azt, hogy egyenlők.
Fordítva sem igaz az, hogy a k. deriváltak folytonosságából következik a k. rendű geometriai folytonosság, azaz 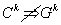 . Ennek belátásához vizsgáljunk meg egy egyszerű kétdimenziós példát! Legyen két görbénk! Az egyik a (3.8)-nak megfelelő
. Ennek belátásához vizsgáljunk meg egy egyszerű kétdimenziós példát! Legyen két görbénk! Az egyik a (3.8)-nak megfelelő
|
|
(3.8) |
a másik (3.9)-nek felel meg.
|
|
(3.9) |
Könnyen ellenőrizhető, hogy a csatlakozó függvények a t=0 időpontban folytonosan differenciálhatók (C 1 ), azonban a (3.6. ábra) ábrán jól láthatóan geometriailag nem folytonosak.
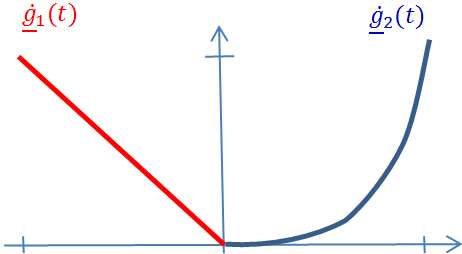
3.3.3. Az elsőfokú paraméteres görbeszakasz leírása
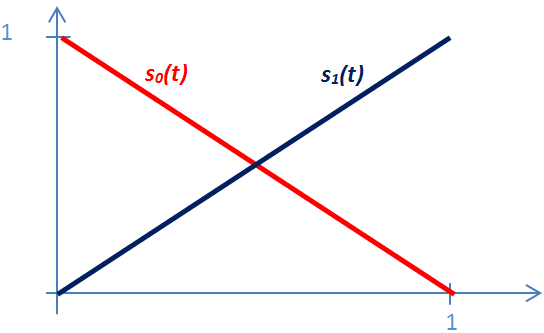
Legyen adva a térben egy szakasz két végpontjával! Ekkor a szakasz belső pontjai felírhatók mint a két végpont súlyozott közepe a  paramétertől függő, változó súlyokkal a (3.10) szerint. A változó súlyok biztosítják azt, hogy t=0 időpont az egyenes szakasz
P
0
pontját, a t=1 időpont az egyenes szakasz
P
1
pontját, a köztes t értékek pedig a szakasz belső pontjait azonosítják (3.7. ábra).
paramétertől függő, változó súlyokkal a (3.10) szerint. A változó súlyok biztosítják azt, hogy t=0 időpont az egyenes szakasz
P
0
pontját, a t=1 időpont az egyenes szakasz
P
1
pontját, a köztes t értékek pedig a szakasz belső pontjait azonosítják (3.7. ábra).
|
|
(3.10) |
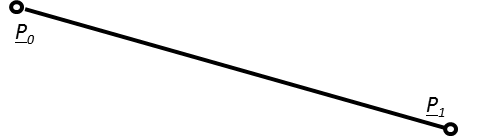
Ilyenkor a pontkoordinátákat szorzó függvényeket súlyfüggvényeknek hívjuk (3.11).
|
|
(3.11) |
Érdemes a súlyfüggvények azon tulajdonságát megfigyelni, hogy az s 0 (0)=1 és s 0 (1)=0, valamint az s 1 (0)=0 és s 1 (1)=1. (3.8. ábra)
A (3.10) egyenlet átírása
|
|
(3.12) |
ugyanez koordinátánként
|
|
(3.13) |
amit átírhatunk mátrixos alakra
|
|
(3.14) |
azaz
|
|
(3.15) |
Definició: A pontok koordinátáit tartalmazó 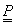 mátrixot (3.16) a geometriát jellemző mátrixnak hívjuk
mátrixot (3.16) a geometriát jellemző mátrixnak hívjuk
|
|
(3.16) |
Definició: A t paraméter hatványait (jelen esetben csak 0 és 1) tartalmazó T vektort paramétervektornak hívjuk (3.17)
|
|
(3.17) |
Definició: A súlyfüggvények együtthatóiból adódó 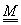 mátrixot a közelítés bázismátrixának hívjuk (3.18).
mátrixot a közelítés bázismátrixának hívjuk (3.18).
|
|
(3.18) |
A (3.15) egyenlet mátrixos formája tehát
|
|
(3.19) |
Egy térgörbét legegyszerűbben törtvonalakkal ábrázolhatunk. Ha adott r 0 , r 1 , …r m térbeli ponthalmazunk, akkor választhatunk úgy paraméterpontokat, hogy a t i+1 -t i =1 legyen, és ekkor a t=t-t i paraméterezéssel bármely két pont között (3.11) súlyfüggvényeivel felírhatjuk a pontokat összekötő törtvonalakat.
3.3.4. Hermite-féle harmadfokú görbeszakasz
Legyen adott két pont a térben, és mindkét pontban egy-egy vektor (3.9. ábra)! Keressük azt a görbét, amelyik kezdőpontja az egyik pont ( P 1 ), végpontja a másik ( P 4 ), míg kezdőérintője ( R 1 ) és végérintője ( R 4 )!

Ez az előírás koordinátánként négy adatot, négy egyenletet és ezzel egy harmadfokú görbét határoz meg. A négy adat:
|
|
(3.20) |
Ha az Hermite-féle görbeszakaszt (3.19) formában szeretnénk felírni, akkor ismerjük a geometriát leíró (3X4 méretű, a pontok és a vektorok által meghatározott) mátrixot és a (4x1 méretű) paramétervektort, a 4x4 méretű bázismátrix azonban ismeretlen.
|
|
(3.21) |
A bázismátrix elemeinek meghatározásához elegendő a (3.21) egyenletekből csak az 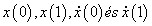 koordinátákra megfogalmaznunk.
koordinátákra megfogalmaznunk.
|
|
(3.22) |
Írjuk át (3.22) négy egyenletét egyetlen mátrixegyenletté!
|
|
(3.23) |
Azt látjuk, hogy bármely peremhelyzetet megvalósító vektor megszorozva egy mátrixszorzattal önmagát adja. Ez azt jelenti, hogy
|
|
(3.24) |
ahol 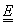 az egységmátrix. Így
az egységmátrix. Így
|
|
(3.25) |
Ha kiszámítjuk az inverzet, akkor azt kapjuk, hogy
|
|
(3.26) |
azaz
|
|
(3.27) |
Az Hermite-féle szakasz tehát:
|
|
(3.28) |
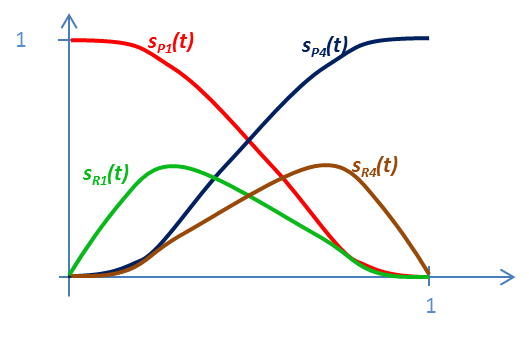
Az Hermite súlyfüggvények viselkedése hasonló a lineáris szakasz súlyfüggvényeihez. Az s
P1
(0)=1 és az s
P1
(1)=0, az s
P4
(0)=0 és s
P4
(1)=1. Hasonlóan a deriváltak súlyfüggvényeire igaz, hogy 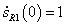 és
és 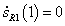 , valamint
, valamint 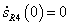 és
és 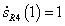 (3.10. ábra).
(3.10. ábra).
3.3.5. Bezier-féle harmadfokú görbeszakasz
A harmadfokú Bezier-görbét a síkban négy pont határozza meg. A kezdőpont az első pont, a végső pont pedig a negyedik. A kezdő érintőt az első és második pont határozza meg, a záró érintőt a harmadik és a negyedik pont definiálja, méghozzá úgy, hogy a pontok közti vektor éppen az érintő (derivált) háromszorosa (3.11. ábra).
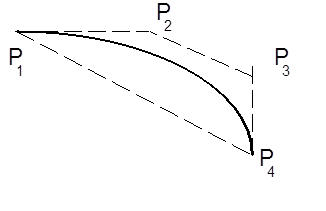
Gondoljunk vissza az Hermite-görbére, amely használta a két végpontot ( P 1 és P 4 ), valamint a két érintőt ( R 1 és R 4 ). Határozzuk meg a Hermite-féle érintőket úgy, hogy
|
R 1 =3 * ( P 2 -P 1 ) R 4 =3 * ( P 4 - P 3 ) |
(3.29) |
legyen! Ekkor a fenti (3.29) egyenlet felírhatjuk az alábbi formában is:
|
|
(3.30) |
azaz
|
|
(3.31) |
ezért a (3.31) egyenlet jobb oldalán a mátrixot – ami áttér az Hermite tartópontokról a Bezier tartópontokra – nevezzük 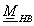 -nek! A (3.19) egyenlet jelöléseivel az Hermite görbére
-nek! A (3.19) egyenlet jelöléseivel az Hermite görbére
|
|
(3.32) |
Ezt viszont átírva (3.31) alapján
|
|
(3.33) |
azaz
|
|
(3.34) |
(3.33) és (3.34) egyenletek összevetéséből és a megfelelő mátrixok behelyettesítésével (3.26) és (3.31) egyenletekből
|
|
(3.35) |
A Bezier-görbe súlyfüggvényei tehát
|
|
(3.36) |
amelyek éppen a
|
|
(3.37) |
binom kifejezés egyszerűsítés nélküli hatványozásából adódó tagok. Vegyük észre azonban, hogy a (3.37) egyenletben szereplő binom azonosan 1, azaz a súlyfüggvények összege 1!
|
|
(3.38) |
A Bezier-görbe tehát mindenhol a P i pontok által kifeszített térbeli (!) négyszögön belül halad, mint ahogyan azt a (3.11) ábra síkbeli esete is mutatja.
Ha a binom modellt tekintjük, akkor a Bezier-görbe a lineáris szakasz általánosítása ((1-t)+t) binom tagjai a súlyfüggvények. Ha harmadfok fölé megyünk, akkor azt mondhatjuk, hogy az
|
|
(3.39) |
kifejtés tagjait tekintjük, amelyek a binom kifejtési szabályai szerint
|
|
(3.40) |
Tehát az n-ed fokú Bezier-görbe súlyfüggvényei éppen az n-ed fokú Bernstein-polinomok [3.3.] . Természetesen a magasabb-fokú Bezier-szakaszt több tartóponttal jellemezhetjük.Az eddigiekben kizárólag egyszerű görbeszakaszokat vizsgáltunk. Kérdés, mit tegyünk, ha több ponton keresztül szeretnénk görbét fektetni?
3.3.6. Természetes spline
A spline-on polinom görbékből összeállított térgörbe. Térbeli pontok sorozatára fektetett egyenes szakaszok elsőfokú spline-t definiálnak. Az n-edfokú spline-ban legfeljebb n-edfokú polinomszakaszok csatlakoznak egymáshoz úgy, hogy rendszerint nemcsak a folytonosságot, hanem az n-1-szeri differenciálhatóságot is megköveteljük.
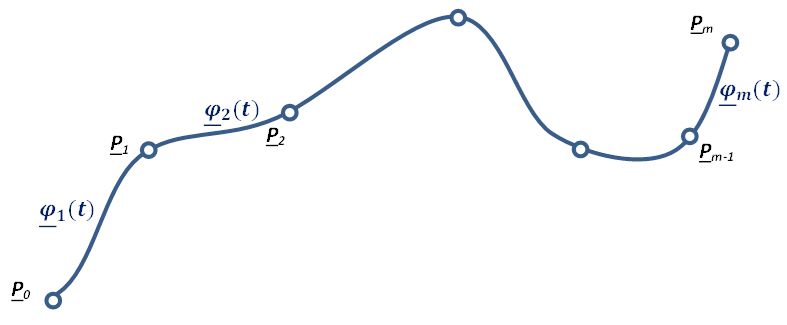
A magasabb fokú spline-ok közül a legelterjedtebb a harmadfokú természetes spline, hogy miért arra később fény derül. Térbeli pontokon áthaladó térgörbére (3.12. ábra) koordinátánként fektethetünk spline görbét. Legyen adott a 3.12. ábra szerint m darab térbeli pont! Keressük azokat a 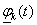 függvényeket (k=1…m), melyek olyanok, hogy a
függvényeket (k=1…m), melyek olyanok, hogy a 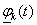 függvény a
P
k-1
és
P
k
pontok között halad, és a görbe belső pontjaiban kétszer folytonosan differenciálható módon csatlakoznak egymáshoz.
függvény a
P
k-1
és
P
k
pontok között halad, és a görbe belső pontjaiban kétszer folytonosan differenciálható módon csatlakoznak egymáshoz.
Csak az x-koordinátára írjuk fel a közelítést, természetesen hasonlóan felírható y- és z-koordinátákra is. Adottak tehát a
|
|
(3.41) |
pontok, ahol 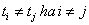 , és
, és 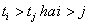 . Keressük azokat a
. Keressük azokat a
|
|
(3.42) |
függvényeket, melyek teljesítik az alábbi interpolációs feltételeket
|
|
(3.43) |
és
|
|
(3.44) |
Azaz az összes görbe átmegy az őt megelőző indexű ponton, és az utolsó görbe az utolsó pontba fut. Illesztési feltételként megfogalmazható, hogy
|
|
(3.45) |
Azaz a belső pontokban a görbeszakaszok folytonosan csatlakoznak egymáshoz. Ugyanezen pontokban előírhatjuk a t szerinti deriváltak folytonosságát is,
|
|
(3.46) |
illetve a t szerinti második deriváltak folytonosan csatlakoznak egymáshoz.
|
|
(3.47) |
(3.43)-(3.47) egyenletek száma m+1+3 * (m-1), amiből az m darab görbe 4 * m ismeretlen paraméterét szeretnénk meghatározni, ezért két további peremegyenletet is hozzáveszünk egyenleteinkhez.
|
|
(3.48) |
|
|
|
(3.49) |
azaz a görbe a két szélen 0 görbülettel távozik.
A görbe meghatározásának első lépéseként nevezzük g k ismeretlen változónak a görbületeket az illesztési pontokban!
|
|
(3.50) |
és
|
|
(3.51) |
Mivel harmadfokú görbéket keresünk, ezek második deriváltja lineáris
|
|
(3.52) |
Ezeket kétszer integrálva, és az integrálási állandókat az illesztési feltételekből az alábbi ún. Clapeyron-egyenlet adódik [3.4.] .
|
|
(3.53) |
Ugyanezt a Clapeyron-egyenletrendszert ismerjük a mechanikából a koncentrált erőkkel terhelt többtámaszú tartók esetéből. Igazából nem meglepő az azonosság, hiszen a koncentrált erőkkel terhelt többtámaszú tartó nyomatéki ábrája szakaszonként lineáris (mint a görbület a spline-oknál). És erre megoldva a rugalmas szál differenciálegyenletét
|
|
(3.54) |
ugyanazt a kétszeri integrálást kell végrehajtanunk, mint a spline-ok esetén. Egyébként a spline szó is innen származik a rugalmas acélszál görbevonalzót használták az angolok a hajótervezésben, és ennek a neve volt a spline.
Érdekes az alábbi Holliday nevéhez köthető tétel [3.4.] .
Tétel: Legyen az adott [t
0
, t
m
] intervallumon t
i
i=0…m nem egybeeső monoton növő pontsorozat értelmezve! Az összes a kérdéses intervallumon kétszer folytonosan differenciálható, és a peremeken az 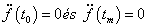 peremfeltételt kielégítő pontok közül a pontokon átmenő harmadfokú spline függvény esetén minimális az
peremfeltételt kielégítő pontok közül a pontokon átmenő harmadfokú spline függvény esetén minimális az
|
|
(3.55) |
integrál.
A (3.55) integrál a második t-derivált négyzetét, a görbület négyzetével rokon adatot integrál. Azt mondhatjuk tehát, hogy az összes ilyen, a pontokon átmenő, a feltételeket teljesítő függvény közül a természetes spline „tekereg” a legkevésbé [3.5.] .
Az a probléma a természetes spline-nal, hogy meg kell oldanunk egy a tartópontok számánál kettővel kisebb ismeretlent tartalmazó lineáris egyenletrendszert (3.53), ami akkor is időigényes, ha az együtthatómátrix ritka. Tetézi a bajt, hogy a spline sajátossága az is, ha bármelyik tartópont elmozdul, akkor a teljes görbe megváltozik, azaz az így megadott görbe csak lokálisan nem módosítható. Kérdés, mit kell egyszerűsítenünk az interpolációs közelítésen ahhoz, hogy lokálisan módosítható, kis számításigényű görbét kapjunk.
3.3.7. Catmull-Rom görbék, a kardinális spline
Ha pontok sorozatára úgy fektetünk interpolációs görbét, hogy a görbe átmegy a pontokon, és minden pontban a görbe érintője arányos a két szomszédos pont által meghatározott vektorral, akkor ezt a görbét kardinális spline-nak nevezzük. Ha a görbe idő szerinti paraméteres leírását tekintjük, akkor azt mondhatjuk, hogy a t k . időpontban a görbe éppen a P k ponton halad keresztül (3.13. ábra). A görbe érintője a t k . időpontban V k , akkor az érintőt a (3.56) egyenlet határozza meg.
|
|
(3.56) |
ahol f(<1) a görbe feszítése. Ha f=0, akkor az éppen a Catmull-Rom spline [3.6.] .
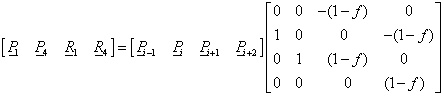
Ha a kardinális spline súlyfüggvényeit szeretnénk kiszámítani, ugyanúgy kell eljárnunk el, mint ahogy a Bezier-súlyfüggvények meghatározásánál tettük. Legyenek a P i és a P i+1 pontok körötti görbeszakasz Hermite geometriai adatai a P 1 , P 4 , R 1 és R 4 vektorok (az ábrán pirossal), melyek a (3.57) alapján megadhatók, mint P i-1 , P i , P i+1 és P i+2 pontok függvényei
|
|
(3.57) |
A (3.57) egyenletben látható mátrix éppen az Hermite-görbéről a kardinális görbére áttérő 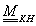 transzformáció.
transzformáció.
|
|
(3.58) |
Elvégezve a kijelölt mátrixszorzást
|
|
(3.59) |
A kardinális spline paraméteres leírását a (3.60) egyenletek tartalmazzák.
|
|
(3.60) |
Szokás a szélen az egyoldalas differeciával számítani az érintőt, és ilyenkor a görbe minden ponton átmegy. A kardinális spline-ok használatának előnye az, hogy nincs szükség egyenletrendszer megoldására, a görbe minden ponton átmegy. Hátránya az, hogy csak egyszer deriválhatók folytonosan.
3.3.8. B-spline-ok
Amennyiben ragaszkodunk a kétszer folytonosan differenciálható spline görbékhez, akkor azt a megkötést kell feladnunk, amely megköveteli, hogy a görbe menjen át a tartópontokon. Definiáljuk először a B-spline fogalmát! Adott fokszámú, adott simaságú, egymáshoz kapcsolódó spline görbeszakaszok egyértelműen leírhatók B-spline függvények lineáris kombinációjaként. Ez azt jelenti, hogy a B-spline-ok a spline függvények bázisaként fogható fel.
Definíció: Legyen adott m+1 darab időpont nem csökkenő sorozata!
|
|
(3.61) |
n. fokú B-spline bázisfüggvényeknek nevezzük azt az m-n darab görbét, melyek az alábbi Cox-de Boor rekurzióval definiálhatók:
|
|
(3.62) |
Mivel az időpontok között megengedtük az egyenlőséget, ezért előfordulhat, hogy a kijelölt művelet nem értelmezhető. Ezért kikötjük, hogy a 0/0 osztás 0-t ad eredményül.
Definíció: Legyenek adottak a
P
0
,
P
1
, …
P
m
pontok a térben és m+1 darab paraméterérték  . A tartópontok által meghatározott, [t
0
,t
m
] paramétertartományon értelmezett n. fokú B-spline görbének nevezzük a (3.62) bázisfüggvényeivel definiált
. A tartópontok által meghatározott, [t
0
,t
m
] paramétertartományon értelmezett n. fokú B-spline görbének nevezzük a (3.62) bázisfüggvényeivel definiált
|
|
(3.63) |
görbét.
A B-spline definíciója alapján az adott tartópontok közül n+1 határoz meg egy n.-ed fokú B-spline görbeszakaszt. A Q i görbeszakaszok előállíthatók, mint a b j,n Cox de Boor rekurzióval meghatározott bázis B-spline-ok – mint súlyfüggvények – lineáris kombinációjával.
|
|
(3.64) |
Szokás még a B-Spline görbéket azért is előnyben részesíteni, mert invariánasak az affin transzformációra. Ez más szavakkal azt jelenti, hogy ha a van egy B-spline-okkal közelített térgörbém, és azt leképezem egy síkra, akkor nem szükséges a görbe „összes” pontját síkba vetíteni, hanem elegendő csak a tartópontokat vetíteni és a síkban meghatározni a görbét [3.7.] .
A B-spline görbék általános vizsgálata helyett tekintsük a harmadfokú görbék esetét!
3.3.8.1. Harmadfokú B-Spline görbék
A 3.3.6. szakasz fejezetben láttuk, hogy a harmadfokú görbék kiemelt fontossággal bírnak.
3.3.8.1.1. A harmadfokú bázisgörbék jellege
Vizsgáljuk meg először az általánosan elterjedt harmadfokú B-spline-okat! A (3.14. ábra) ábrán világoskékkel a b j,1 tag, sötétkékkel a b j,2 tag, zölddel a b j,3 és végül pirossal a b j,4 tag(ok) láthatók.

Ha egyenközű B-spline görbéket használunk, a bázisfüggvények is egyszerűsödnek. Legyen t 0 =-3, t 1 =-2, t 2 =-1 és t 3 =0 és t 4 =1! Ekkor a bázisfüggvények könnyen számíthatók:
|
|
(3.65) |
3.3.8.1.2. Közelítés harmadfokú B-spline görbével
A B-spline (3.66) képlete szerint a harmadfokú Q i görbeszakaszok előállíthatók, a b j,3 Cox de Boor rekurzióval meghatározott bázis B-spline-ok – mint súlyfüggvények – lineáris kombinációjával.
|
|
(3.66) |
Ha (3.66) képletet n=3 értékre (harmadfokú B-Spline-okra) alkalmazzuk, és használjuk a t=t-t i helyettesítést, akkor a súlyfüggvények egy szakaszon olyanok lesznek, mint amit a 3.14. ábra [t 3 ,t 4 ] szakaszán láthatunk, illetve ha kiszámítjuk a súlyfüggvényeket, akkor a
|
|
(3.67) |
kifejezéshez jutunk, azaz írhatjuk, hogy
|
|
(3.68) |
ahol
|
|
(3.69) |
és
|
|
(3.70) |
Ha kiszámítjuk a (3.67) súlyfüggvények összegét, akkor
|
|
(3.71) |
ugyanúgy, mint a Bezier splineoknál. Ez azt jelenti, hogy a B-Spline szakasz is benne halad a tartópontok által meghatározott térbeli négyszögben (3.15. ábra).
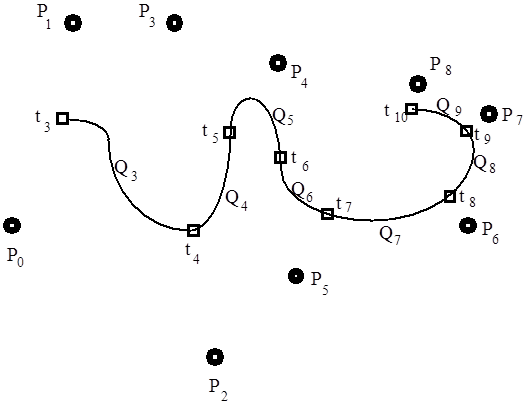
Vizsgáljuk meg a harmadfokú B-spline folytonossági viszonyait! Az i. ponthoz tartozó görbe
|
|
(3.72) |
alakban írható. Ebből csak az x-koordinátákra felírva a csatlakozó görbék adatait (y, és z ugyanígy alakul):
|
|
(3.73) |
tehát a görbe folytonos. Hasonlóan a deriváltakra azt kapjuk, hogy
|
|
(3.74) |
tehát a görbe folytonosan differenciálható. A második deriváltak is egyenlők lesznek
|
|
(3.75) |
A B-spline görbéket tehát tartópontjaikkal irányíthatjuk és a görbe kétszer folytonosan differenciálható módon követi a pontok helyzetét, de nem megy át rajtuk. Kérdés, hogy mi történik akkor, amikor két szomszédos pont egybeesik. A (3.71) egyenlet szerint a súlyfüggvények összege azonosan egy, tehát a görbeszakasz benne halad a befoglaló négyszögben (3.16. ábra ábra bal oldala). Ha két szomszédos tartópont egybeesik, akkor a befoglaló négyszög háromszöggé torzul. A görbe benne halad a háromszögben, és a két egybeeső pont nagyobb „súlyával” közelebb „húzza” magához a görbét (3.16. ábra középső ábra). Végül, ha a három szomszédos pont esik egybe, akkor a befoglaló négyszögek egyenes szakaszokká torzulnak, és a B-spline is két csatlakozó egyenes szakasszá torzul (3.16. ábra ábra jobb oldala).
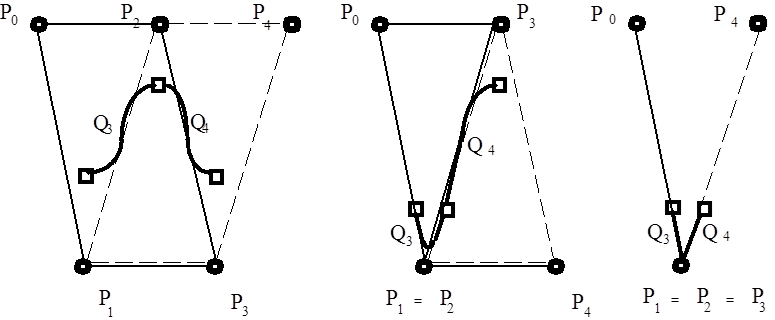
Ha (3.67) alapján felírjuk az egyenes szakaszokra torzult első B-spline-t, akkor adódik, hogy
|
|
(3.76) |
Ami valóban egy egyenes paraméteres egyenlete, azonban (3.10)-zel ellentétben a paraméterfüggvények nem lineárisak. Ez is egy példa arra, hogy a kétszer folytonosan differenciálható függvény geometriailag nem folytonos.
3.3.8.2. Közelítés harmadfokú nem egyenközű B-Spline görbékkel
Ha a (3.62) Cox de Boor rekurziót harmadfokú függvényre írjuk fel, akkor képleteink a (3.77) szerint alakulnak.
|
|
(3.77) |
Ha kiszámítjuk a t 0 =t 1 =t 2 =t 3 =0, t 4 =t 5 =t 6 =t 7 =1 időosztásra a B-spline együtthatókat,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
akkor b 0,3 (t), b 1,3 (t), b 2,3 (t) és b 3,3 (t) éppen a Bezier súlyfüggvények.
3.3.8.3. Interpoláció B-Spline görbékkel
A természetes spline görbének azt az előnyét elvesztettük, hogy átmegy a megadott pontokon. Szerencsére nem végleg. Az egyenletrendszer megoldását azonban nem spórolhatjuk meg. A B-spline görbékkel való interpoláció alapgondolata az, hogy ha adottak a pontok, amelyeken a B-spline görbének át kell mennie, akkor keressünk olyan tartópontokat és a hozzájuk tartozó csomópontértékeket úgy, hogy a görbe áthaladjon pontjainkon. A probléma az, hogy végtelen sok megoldás létezik.
Tegyük fel, hogy adott m+1 darab térbeli pontunk
Q
i
i=0,1,…m! Ha ismerjük a
Q
i
pontokhoz tartozó 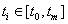 B-spline paraméterpontokat, akkor (3.63)-nak megfelelően felírhatjuk az n.-edfokú B-spline képletét az összes m+1 pontra. Ekkor az
B-spline paraméterpontokat, akkor (3.63)-nak megfelelően felírhatjuk az n.-edfokú B-spline képletét az összes m+1 pontra. Ekkor az
|
|
(3.78) |
3*(m+1) egyenletrendszer adódik, melynek 3*(m+1) ismeretlenje a P i pontok koordinátái [3.8.] .
A probléma, hogyan vegyük fel a paraméterpontokat. Erre több módszer is kínálkozik.
3.3.8.3.1. Egyenletes időosztás
A legegyszerűbb az egyenletes időosztás, amikor
|
|
(3.79) |
Természetesen, hogy ez mennyire lesz hullámos, az függ a pontok elhelyezkedésétől. Ezt a módszert ritkán használják.
3.3.8.3.2. Osztás poligonkerület ívhossza szerint
Legyen a megadott pontokat egyenes szakaszokkal összekötő poligon ívhossza
|
|
(3.80) |
A köztes tartópontokat a tartóponthoz vezető poligonkerület és teljes poligonkerület hányadosa határozza meg.
|
|
(3.81) |
Az ívhossz módszer általában jól működik. Ha hosszú poligonélet használunk, az hullámzási problémát okozhat.
3.3.8.3.3. Centripetális módszer
Legyen egy a>0 érték! A megadott pontokat egyenes szakaszokkal összekötő poligon éleivel számítsuk ki az
|
|
(3.82) |
értéket, és ezzel a paraméterosztás legyen
|
|
(3.83) |
Ha a=0.5, akkor ez egy közelítése a kanyarban való haladáshoz szükséges centripetális erőnek. Az a=1 érték az ívhossz-módszerhez vezet.
3.3.8.4. Racionális, nem egyenközű B-spline (Non-Uniform Rational B-Spline - NURBS)
Az eddig megismert görbeközelítési módszerek mindegyike polinommal közelítette a koordináta-függvényeket. Ha áttérünk homogén koordinátás ábrázolásra, akkor minden 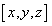 pont helyett az
pont helyett az 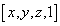 homogén koordinátákkal definiált pontot használjuk (lásd 3.2. szakasz fejezet). Ez azt jelenti, hogy paraméteres megadáskor az
homogén koordinátákkal definiált pontot használjuk (lásd 3.2. szakasz fejezet). Ez azt jelenti, hogy paraméteres megadáskor az
|
|
(3.84) |
egyenleteket használhatjuk, ahol a w(t) minden egyes megadott paraméterpontban 1. Azaz 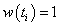 . Ekkor az a pontkoordináták
. Ekkor az a pontkoordináták
|
|
(3.85) |
ami azt jelenti, hogy racionális törtfüggvényekkel írtuk le a görbét.
3.3.9. Szabadformájú felületek
A görbékhez hasonlóan a felületeket is függvényekkel közelítjük
3.3.9.1. Felületek leírása háromszöghálókkal
Háromszöget definiálhatunk a háromszög csúcspontjaival r 1 , r 2 és r 3 . Ekkor a háromszög belső pontjai leírhatók u, v koordinátákkal úgy, hogy a sarokpontok koordinátáinak súlyozott összegét számítjuk, úgy hogy a súlyok összege 1 legyen.
|
|
(3.86) |
Ha egy felületet szeretnénk ábrázolni, akkor lehetőségünk van a háromszögek csúcspontjait összegyűjteni egy koordinátákat tartalmazó tömbben (3.87).
|
|
(3.87) |
A felület geometriájának leírása ezek után egy olyan tömbben történhet, amely a háromszögek csúcspontjait (i,j,k) úgy tartalmazza, hogy egy háromszöghöz három, a csúcspontok tömbjére mutató indexet tartalmaz, melynek alapján a háromszög csúcspontjainak koordinátái kereshetők.
|
|
(3.88) |
Ha megvilágítottan és árnyalva szeretnénk megjeleníteni a felületet, akkor szükségünk van a felület normálvektorára. A háromszög három pontja meghatározza a sík normálvektorát. Azonban így egyik háromszögről a másikra áthaladva a normálvektor nem folytonosan változik, ezért az élek kiemelődnek. Elkerülhetjük ezt a jelenséget, ha minden ponthoz egy normálvektort is tárolunk (3.89).
|
|
(3.89) |
A háromszögön a konstans normálvektor helyett (3.86)-nak megfelelő, folytonosan változó normálvektort használunk.
Lehetőség van arra is, hogy anyagok tömbjét is mentsük, és minden háromszöghöz egy anyagot rendeljünk, illetve, hogy ugyanígy mintázatot is rögzítsünk a felületre.
3.3.9.2. Spline felületek
A
Q
(t) térgörbék leírásánál (3.19) használtuk a 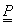 geometriát jellemző mátrixot, a közelítés bázismátrixát
geometriát jellemző mátrixot, a közelítés bázismátrixát 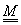 és a paramétervektort
és a paramétervektort 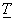 .
.
3.3.9.2.1. Harmadfokú Hermite-felületfolt
Próbáljunk egy felületet leírni úgy, hogy a
Q
(t) Hermite típusú térgörbét egy másik, független s paraméter mentén változtatjuk. Ekkor
Q
(s, t) kétparaméteres felület leírását kapjuk. Tegyük ezt úgy, hogy a 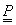 geometriát jellemző mátrix vektorait s-től függővé tesszük.
geometriát jellemző mátrix vektorait s-től függővé tesszük.
|
|
(3.90) |
A 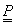 geometriát jellemző mátrix oszlopai térbeli vektorok. Ezek a vektorok előállíthatók hasonló módon, mint a görbék (3.19)-hez hasonló módon.
geometriát jellemző mátrix oszlopai térbeli vektorok. Ezek a vektorok előállíthatók hasonló módon, mint a görbék (3.19)-hez hasonló módon.
|
|
(3.91) |
azaz
|
|
(3.92) |
ebben a 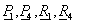 vektorok helyett csak azok x koordinátáit használva
vektorok helyett csak azok x koordinátáit használva
|
|
(3.93) |
(3.93)-t (3.92)-be helyettesítve
|
|
(3.94) |
A Q y (s,t) és a Q z (s,t) görbék ugyanígy felírhatók.
3.3.9.2.2. Harmadfokú Bezier-felületfolt
A görbékhez hasonlóan, ha át kívánunk térni egyik ábrázolási módról a másikra, akkor nincs más dolgunk, mint a bázismátrixot szorozni az egyik bázisról a másikra való áttérés mátrixával. Így a Bezier-féle felületfolt Q
x
(s,t) leírása adódik. Az Hermite-féle bázismátrixot az x, koordinátákra 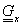 -el jelölve (
-el jelölve (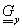 , és
, és 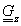 hasonlóan felírható) adódik a Bezier-felületfolt egyenlete (3.95).
hasonlóan felírható) adódik a Bezier-felületfolt egyenlete (3.95).
|
|
(3.95) |
azaz
|
|
(3.96) |
A 3.17. ábra a felületfolt 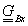 ,
, 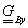 ,
, 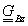 Bezier féle geometriát jellemző mátrixok koordinátáiból alkotott tartópontok láűthatók.
Bezier féle geometriát jellemző mátrixok koordinátáiból alkotott tartópontok láűthatók.
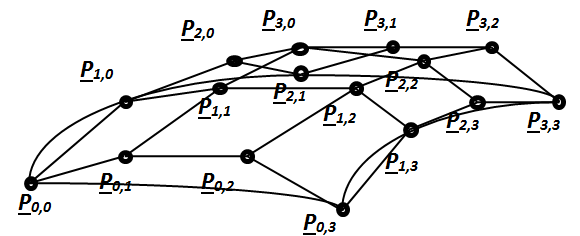
3.3.9.2.3. Felületfoltok illesztése
Ha két felületfoltot szeretnénk a 3.18. ábra szerint egy peremen G 1 folytonosan illeszteni, akkor az A felületfolt mindegyik koordinátára vonatkozó geometriai mátrix s=1 paramétert leíró elemei (a mátrix második sora) megegyeznek a B felületfolt s=0 paraméterű élet meghatározó elemeivel (a mátrix első sora). Ez biztosítja a C 1 folytonosságot. Hasonlóan a G 1 folytonossághoz a B felületfolt s=0 élén a t irányú parciális deriváltak (a mátrix harmadik sora) megegyeznek az A felületfolt s=1 paraméterű élén számított t irányú deriváltak (a mátrix negyedik sora) konstanszorosával (3.18. ábra).
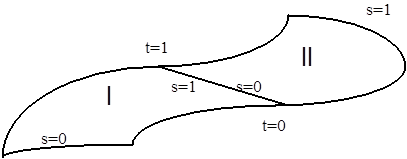
|
|
(3.97) |
3.3.9.2.4. Harmadfokú B-spline felületek
k*n-edfokú B-spline felületnek nevezzük a tartópontok s sora és o oszlopa által meghatározott függvényt.
|
|
(3.98) |
3.3.10. Testek
Testnek nevezzük a háromdimenziós tér olyan részhalmazait, amelyeknek nincsen elfajuló alacsonyabb dimenziós része (például egy síkidom) [3.6.] . Kérdés, hogyan írhatjuk le a testek geometriáját? Erre többféle lehetőségünk is van. Hozzáállhatunk a probléma megoldásához úgy, hogy egyszerű résztestekből építkezünk – leírjuk a test határait, vagy megadjuk, hol vannak a térben a testnek pontjai.
3.3.10.1. CSG modellek
A legrégebb módszer még a számítógépes grafika hőskorából származik. A CSG (Constructive Solid Geometry) elv alapgondolata, hogy vannak paraméterezhető alapgeometriáink, mint a tégla, a gömb, a (csonka)gúla, a (csonka)kúp stb. Ezeket elhelyezzük a valós tér modelljében, és ezek között logikai műveleteket végzünk (unió, metszet és különbség). A 3.19. ábra egy „fenyőfatalp” modellezését mutatja be. Két tégla uniója a kereszt, amiből egy henger kivonása modellezi a furatot.
A CSG modellezés ma is része minden CAD rendszer felhasználói felületének, még akkor is, ha már nem így modelleznek a tervező programok.
3.3.10.2. B-Rep testábrázolás
A B-Rep szó a Boundary Representation angol kifejezés rövidítése, határábrázolást jelent. Azt takarja a fogalom, hogy egy testet ábrázolhatunk felületeivel és a felületek test felé mutató normálisaival. A topológiai leírás nehezebb, de könnyen készíthető szabálytalan geometriájú, szabadformájú felületek által határolt test. A modern CAD rendszerek alkalmazzák ezt a technikát
3.3.10.3. Térfogati modellek
A térfogati modell a tér pontjaihoz hozzárendelt sűrűségfüggvény [3.6.] . Ezt alkalmazzák a méréseknél, a CT- és MRI felvételeknél. Ábrázolása rácsban (térbeli lépcsősfüggvény) történik. Ez a bitkép raszteres modelljének 3D általánosítása. A térbeli raszterpontot voxel-nek nevezzük.
3.4. A megjelenítő cső
A mai képalkotó eszközök raszteres elven működnek, ezért a megjelenítéskor is raszteres eszközön működő grafikus rendszereket vizsgálunk. A (3.20. ábra) ábrát tanulmányozva végigkövethetjük egy 3D-s grafikus rendszer (OpenGL) képalkotási folyamatának lehetőségeit és lépéseit. Az OpenGL hardverfüggetlen programozási felületet biztosító háromdimenziós grafikus alprogram-rendszer, melyet a Silicon Graphics Inc. [3.9.] fejlesztett ki Unix alapú hálózatban működő számítógépekre. Az OpenGL megjelenítési szabvánnyá vált és API függvényhívásait használhatjuk a Windows rendszerekben is.
Az ábra bal oldalán, a belépési ponton látható, hogy lehetőségünk van arra, hogy térbeli objektumokat leíró csúcspontjaikkal (vertex) jellemezve adjunk át megjelenítésre. Közvetlenül elérhetjük a kép pontjait is, így szükség esetén magunk is definiálhatjuk a pixeleken megjeleníteni kívánt információt. Már itt érdemes megemlíteni, hogy az alapobjektumok sorozatát listába szervezhetjük (display lista), amelyet ezek után egyetlen rajzelemként kezel a rendszer.
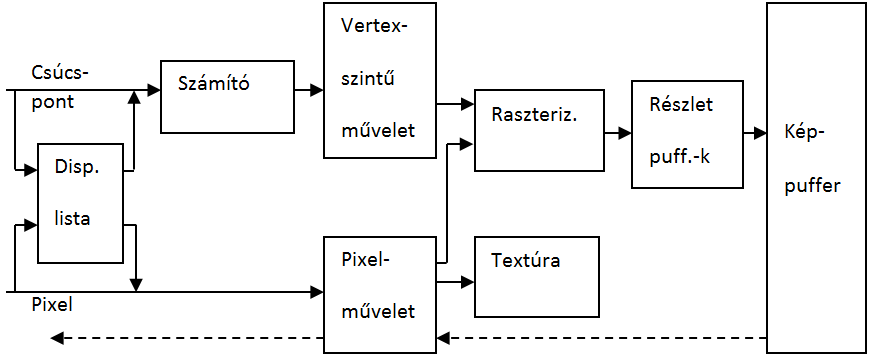
A csúcspontokkal jellemzett térbeli elemek esetén a számító egység feladata, hogy a függvényként megadott térgörbéket és felületeket értelmezze. A vertex-szintű műveleteket végző modul számítja a megvilágítást, az előírt geometriai transzformációkat és kép méretre vágását. Az ilyen módon előkészített kép pontjainak adatait a raszterizáló határozza meg. Akár vektoros szemléletű, szabadformájú felületmodellel is van dolgunk, a megjelenítéshez a felület egyenlete alapján a raszterizáló apró háromszögekre (3.3.9.1. szakasz) bontja a felületeket, és ezeket jeleníti meg. A képpontokat tartalmazó kép további részletpufferekben tárolt adatok segítségével kerül a képernyőmemóriába, megjelenítésre. Ilyen részletpuffert használhatunk a takarások meghatározására (Z-puffer). A színkeverő puffer segítségével áttetsző objektumokat jeleníthetünk meg, ha a színezéskor a háttérszíneket is figyelembe vesszük. A „stencilpuffert” használhatjuk, ha egy képet úgy szeretnénk megjeleníteni, ahogyan azt egy ablakon kitekintve látjuk, amikor az ablakkeretek takarják a kép egyes részeit.
Ahogy az ábrán nyomonkövethető, az OpenGL lehetővé teszi, hogy a megjelenítésre kerülő bitképes adatok közvetlenül a raszterizáló modulhoz kerüljenek. Az OpenGL textúra-megjelenítési lehetősége azt takarja, hogy a térbeli objektumokat bitképpel mintázott anyaggal is beboríthatjuk.
Ismerkedjünk meg először a képernyőn történő megjelenítés geometriai transzformációs hátterével!
3.4.1. A tér leképezése síkra
Térbeli pontokat két alapvető módon vetíthetünk síkba, párhuzamos és centrális vetítősugarakkal.
A párhuzamos sugarakkal való vetítést axonometriának hívjuk. A vetítés matematikai modelljét úgy állíthatjuk fel, hogy az x-y-z térbeli koordináta-rendszer párhuzamosan vetített képét berajzoljuk a ξ-η koordinátarendszerrel bíró síkbeli lapra. Feltételezzük, hogy a térbeli koordináta-rendszer origójának képe a síkbeli koordináta-rendszer origója. A (3.21. ábra) ábrán az x-y-z térbeli koordináta-rendszer képe szaggatott vonallal látszik a folytonos vonallal rajzolt ξ-η koordinátarendszerben. Jelöljük az ábra szerint a ξ-tengely és az x-tengely által bezárt szöget α-val, a ξ-tengely és az y-tengely által bezárt szöget β-val és az η-tengely és a z-tengely által bezárt szöget γ-val! Mivel az x-y-z koordináta-tengelyek nem párhuzamosak a ξ-η síkkal, a koordináta-egységek képe a síkon rövidebbnek látszik. Az x-irányú egység q x (≤1)-nek, az y-irányú q y (≤1) és a z-irányú q z (≤1) hosszúnak látszik.
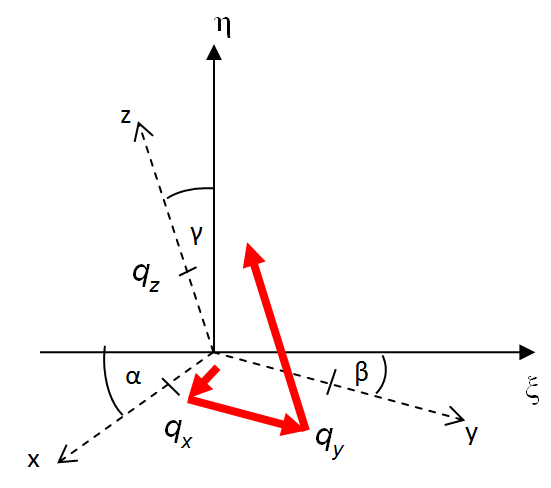
Ha tehát egy (x, y, z) koordinátájú pontnak keressük a (ξ,η) síkbeli koordinátáját, akkor a leképezést megvalósító függvénypár az (f ξ , f η ) (3.99) szerint.
|
|
(3.99) |
A leképezést egyszerűen felírhatjuk ha arra gondolunk, hogy az origóból indulva a koordináta-tengelyek képeivel párhuzamosan, a rövidüléseknek megfelelően haladunk x, y és z egységnyit, akkor az (x,y,z) pont (ξ,η) képébe jutunk (3.21. ábra). Ebből következik, hogy a piros nyilal ξ és az η irányú vetületeit összegezve az alábbi (3.100) módon adódnak a koordináták.
|
|
(3.100) |
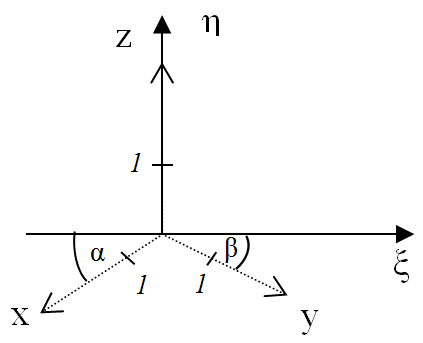
Az axonometria speciális esetei az izometrikus axonometria, amikor az x-y-z koordináta-tengelyek egymással 120°-ot zárnak be, a z-tengely képe az η-tengellyel esik egybe (α=30, β=30, γ=0) és a rövidülések q x =q y =q z =1 (3.22. ábra)
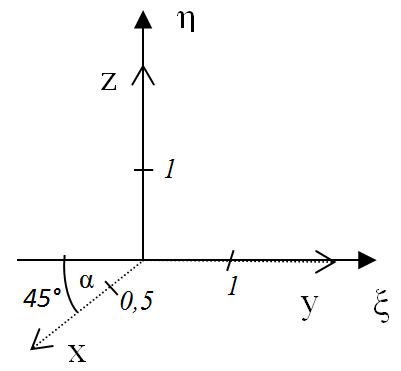
Másik elterjed axonometria a Cavalier-féle, vagy katonai axonometria, ahol a vízszintes y-tengely, a ξ-tengellyel esik egybe a függőleges z-tengely, az η-tengellyel esik egybe, az x-tengely pedig a másik kettővel 135°-os szöget zár be (α=45, β=0, γ=0). A rövidülések: q x =0,5, q y =q z =1.
Az axonometrikus leképzés adott koordináta-irányban távolságtartó. Ezért a kocka hátsó éle ugyanolyan hosszúnak látszik mint az első él. A szemünkkel azonban nem ilyen képet kapunk. A szemünk centrálisan vetít.
Centrális vetítés egy pontba érkező sugarakkal vetíti a képsíkra a térbeli pontokat. Ahhoz, hogy a centrális vetítés egyszerű képleteit megkapjuk, tegyük fel, hogy a térbeli x-y-z koordináta-rendszer pontjait az x-y síkkal párhuzamos S képsíkra vetítjük! Jelöljük a térbeli x-y-z koordináta-rendszer kezdőpontját C-vel. C lesz a vetítés centruma. Az S síkon lévő ξ-η koordináta-rendszer kezdőpontja O, legyen olyan, hogy a térbeli rendszer z-tengelyén d távolságra van C-től! A S sík ξ-η koordináta-rendszerének tengelyei párhuzamosak az x- és y-tengelyekkel (3.24. ábra). Keressük a centrális vetítés (3.99)-nek megfelelő leképezését.
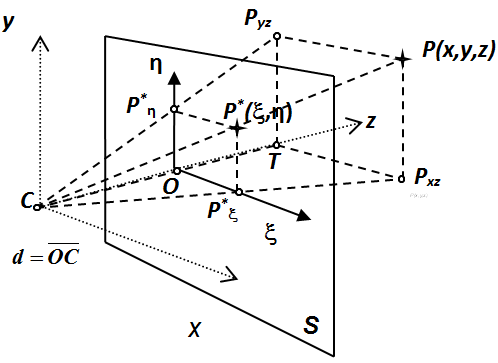
Az ábrán látható módon legyen az origó centrum távolság d! Legyenek egy térbeli P pont koordinátái (x,y,z) és ennek P* képe a síkon (ξ,η) koordinátákkal. P pont vetülete az x-z síkra P xz (ennek a z-tengelytől vett távolsága éppen az x-koordináta), az y-z síkra P yz (ennek pedig a z-tengelytől vett távolsága éppen az y-koordináta). A P xz képe az S síkon P* ξ , és ennek a síkbeli koordinátarendszer kezdőpontjától való távolsága éppen a ξ koordináta. A P yz képe az S síkon P* η és ennek a síkbeli koordináta-rendszer kezdőpontjától való távolsága éppen a η koordináta! Mivel COP* ξ Δ hasonló CTP xz Δ-höz, így
|
|
(3.101) |
azaz
|
|
(3.102) |
Hasonlóan az yz síkban CTP yz Δ hasonló COP η Δ-höz, így
|
|
(3.103) |
azaz
|
|
(3.104) |
Ezzel létrehoztuk a (3.99) leképezést, hiszen átrendezés után
|
|
(3.105) |
adódik. A (3.105) képletekkel az a probléma, hogy a leképezés nem lineáris. Lineárissá tehetjük úgy, hogy megnöveljük a dimenziószámot (kettőről háromra), bevezetve a homogén koordinátákat. Tekintsük a [x, y,z] térbeli pont helyett a négydimenziós [x, y, z, 1] pontokat. Azaz az [x, y, z, w] négydimenziós térben a w=1 háromdimenziós altérben gondolkodunk. Ebben a térben a (3.106) leképezés
|
|
(3.106) |
ami lineáris, hiszen átírható a (3.107) alakra.
|
|
(3.107) |
3.4.2. Window-Viewport transzformáció
Miután a térbeli objektumot leképeztük a síkra, nincs más dolgunk, mint hogy azt a képernyő méreteire skálázzuk. A leképezett kép befoglaló téglalapja (window) nem hasonló a képernyő téglalapjához (viewport). A leképezett kép lehet nagyobb és kisebb, mint a képernyő.
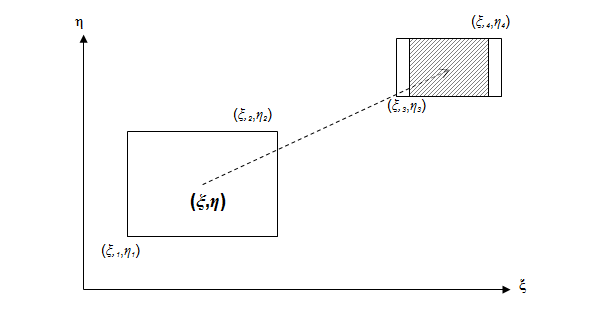
A (3.25. ábra) ábrán a leképezett kép (window) befoglaló téglalap átellenes sarkainak koordinátái a (ξ 1 ,η 1 ) és (ξ 2 ,η 2 ). A megjelenítő befoglaló téglalap átellenes sarkainak síkbeli koordinátái (ξ 3 ,η 3 ) és (ξ 4 ,η 4 ). A leképezés során többféle stratégiát is követhetünk. Készíthetünk leképezést úgy, hogy a window sarkok a viewport sarkokba kerüljenek. Ilyenkor a kép nem méretarányos, de kitölti a képernyőt. Igazíthatjuk a képet a viewport valamelyik sarkához is. A következőkben azt az esetet számítjuk ki, amelyben a leképzett modell középpontja a képernyő középpontjába kerül. A vízszintes képéleket vízszintes képélekhez, vagy függőleges képéleket függőleges képélekhez igazító skálázások közül a kisebbet (amelyik a teljes képet a megjelenítőre viszi) választjuk.
Állapítsuk meg a leképezés nagyítását! Ez a viewport és window a vízszintes oldalainak, valamint a függőleges oldalainak hányadosai közül a kisebb.
|
|
(3.108) |
A leképezés lineáris, amely egy α skálázásból és egy eltolásból áll. Keressük a transzformációt a (3.109) alakban!
|
|
(3.109) |
Mint azt már rögzítettük, azt az esetet számítjuk ki, amelyben a leképzett modell középpontja a képernyő középpontjába kerül. Ebből meghatározhatjuk az ismeretlen 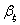 és
és 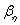 értékeket.
értékeket.
|
|
(3.110) |
azaz
|
|
(3.111) |
3.4.3. A láthatóság
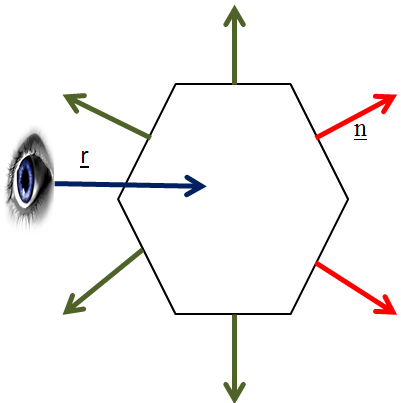
A láthatóság meghatározásának legegyszerűbb módja a hátsó lap eldobásának módszere, aminek alapkoncepciója az, hogy ha a felületet (testet) alkotó háromszögháló kifelé mutató normálisa n egy irányba mutat a ránézés irányával r (3.26. ábra), vagyis n * r> 0 akkor az a háromszög nem látható.
A mélységi rendezés (Depth Sort) algoritmus lényege, hogy rendezzük a képernyőtől (leképezési sík) való távolságuk szerinti sorrendbe a kirajzolandó objektumok felületét alkotó háromszögeket, majd hátulról előre rajzoljuk ki őket. Így amit később rajzolunk ki az átfesti (takarja) a hátrébb lévő elemeket. A probléma a sorbarendezéssel van, mint ahogy azt a 3.27. ábra mutatja.
A mélységi rendezés algoritmusa:
A Δ-kel közelített felület Δ elemeit a megjelenítési síktól mért legtávolabbi pontjuk távolsága szerint rendezzük sorba! Vizsgáljuk meg a sorrend összes háromszögpárjának (A és B) viszonyát! Az A<B sorrend helyes, ha
-
az A Δ legtávolabbi pontja közelebb van a síkhoz, mint B Δ legközelebbi pontja. (Ez mindösszesen számok összehasonlítását jelenti.)
-
A háromszögek befoglaló téglalapjai nem metszik egymást. (Ez kétszer három pont síkbeli koordinátáinak minimum-maximum keresését, és számok összehasonlítását jelenti.)
-
Az A Δ vetített képe nem metszi B Δ vetített képét. (Az A Δ minden oldalára igaznak kell lennie annak, hogy a B Δ összes csúcsa és az A aktuális oldallal szemben fekvő csúcsa az oldalegyenes szembenfekvő oldalára esik)
-
a B Δ mindhárom sarokpontja az A Δ síkja mögött helyezkedik el. (B háromszög összes csúcspontját be kell helyettesíteni A síkjának egyenletébe.)
Ha ezek egyike sem áll fenn, akkor az egyik háromszöget két részre kell vágni, és folytatni a módszert egészen addig, míg az összes háromszög sorbarendezhető.
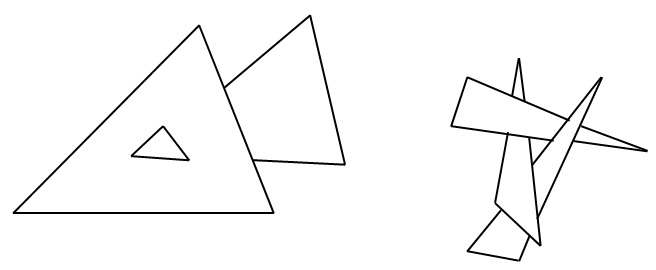
A bináris térfelosztó (BSP - Binary Space Partitioning) algoritmus lényege az, hogy bármely sík három nagy halmazra osztja a tér objektumait: a sík felett lévők (az objektum összes pontja a sík normálvektorával egy irányban vagy a síkon van), a sík alatt lévők (az objektum minden pontja a normálvektorral ellentétes oldalon található) és végül azok az objektumok, amiket a sík elmetsz.
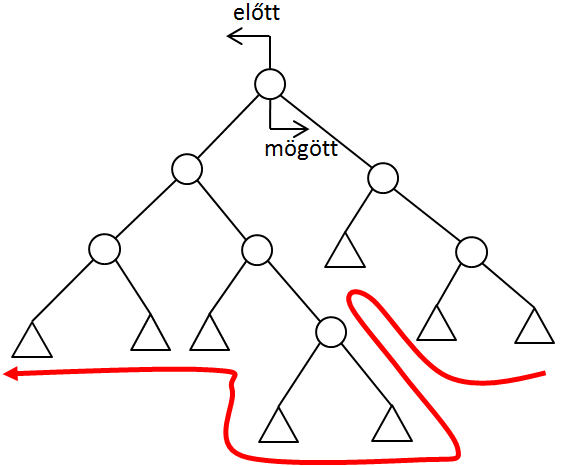
Legyen a testet reprezentáló háló egyik háromszögének síkja az első vágósík! Azokat az elemeket, amelyeket ez a sík kettévág, további háromszögekre bontjuk úgy, hogy ezek már vagy a sík alá vagy fölé kerülnek. Az eljárás rekurzív módon folytatható addig, ameddig a vizsgált halmaz egyetlen háromszögből nem áll. Ha a rekurzív vágásokat egy gráfban ábrázoljuk, akkor bináris fát kapunk, ahol a csomópontok a vágósíkok és a levelek tovább nem bontható háromszögek lesznek. A felbontás végén a leveleket (háromszögeket) hátulról előre (a 3.28. ábra ábrán piros nyíl) kifesthetjük, így az előbb lévő háromszög átfesti a takart elemet.
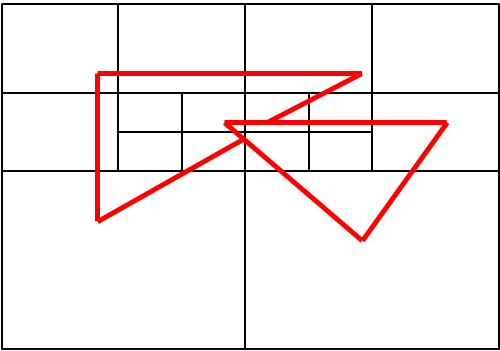
Az területfelosztásos (Area Subdivision) technika lényege az, hogy a Viewportot négy egyenlő részre bontjuk (3.29. ábra). A levetített háromszögek vizsgálata során megállapíthatjuk, hogy készen vagyunk a takarással, ha:
-
a részt egyetlen háromszög foglalja be (3.30. ábra/a. ábra),
-
egyetlen háromszög sincs a negyedben (3.30. ábra/b. ábra),
-
az negyed egyetlen háromszöget metsz, vagy foglal magában (3.30. ábra/c. ábra),
-
valamelyik háromszögről tudjuk, hogy takar (3.30. ábra/d. ábra).
A takart részek eltávolításának manapság már legelterjedtebb algoritmusa a Z-puffer algoritmus. A grafikus kártyák már beépített Z-pufferrel és algoritmussal rendelkeznek, így ha megfelelő 3D-s rendszert használunk, akkor ezzel nincs gondunk. Az algoritmus lényege, hogy minden képernyőpixelhez a Z-puffer tartalmaz egy mélységi adatot. A Z-puffer tehát egy távolságlista, melynek elemei a képernyőpontokhoz tartoznak (3.31. ábra ábra bal oldala). Az algoritmus úgy működik, hogy mielőtt elkezdené a megjelenítést a Z-puffer minden egyes távolságadata a gyakorlati 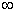 . A kép kirajzolása során minden egyes ponthoz kikereshető az aktuális távolságérték (Z-puffer érték). Ha az aktuális pont távolsága (z-koordináta) kisebb mint a Z-pufferben tárolt érték, akkor a pont kifestődik, és a Z-pufferbe a z-koordináta lesz az új, aktuális érték. Ha a z-koordináta értéke nagyobb, mint ami a Z-pufferben volt, akkor a ponttal és z-koordinátájával semmi teendő (3.31. ábra) jobb oldala. A Z-puffer tehát a kirajzolás során az adott képernyőpontban aktuálisan látható legközelebbi pont z távolságát tartalmazza.
. A kép kirajzolása során minden egyes ponthoz kikereshető az aktuális távolságérték (Z-puffer érték). Ha az aktuális pont távolsága (z-koordináta) kisebb mint a Z-pufferben tárolt érték, akkor a pont kifestődik, és a Z-pufferbe a z-koordináta lesz az új, aktuális érték. Ha a z-koordináta értéke nagyobb, mint ami a Z-pufferben volt, akkor a ponttal és z-koordinátájával semmi teendő (3.31. ábra) jobb oldala. A Z-puffer tehát a kirajzolás során az adott képernyőpontban aktuálisan látható legközelebbi pont z távolságát tartalmazza.
3.5. A képszintézis alapfogalmai
Ha a geometriai modelleket szeretnénk megjeleníteni a számítógép képernyőjén, akkor tisztáznunk kell azokat a fogalmakat, amelyekkel nemcsak a testek geometriáját, hanem annak megvilágítását, a test felületének fényvisszaverő tulajdonságait is modellezhetjük. A modellezés érdekében részletesebben megismerkedünk a fény és a színek tulajdonságaival, a fényforrások egyszerű modellezésével, a testek anyagának fénytani viselkedésének leírásával és végül egy megvilágított térrész megjelenésének komplex modellezésével.
3.5.1. Fénysűrűség
A fluxus definíciószerűen egy adott felületen átáramló energia mennyisége, melynek mértékegysége Watt. Ha a fényáramot v vektor jellemzi, akkor az A felületen áthaladó fluxus ϕ.
|
|
(3.112) |
A fénysűrűség jellemzésére azonban nem jó mérték a fluxus, mert annak mértékét a fénysugár és a felület normálvektorának iránya, valamint a felület nagysága is befolyásolja. Ahhoz, hogy kezelhető mennyiséget kapjunk, szükséges a látószög térbeli általánosítása, a térszög.
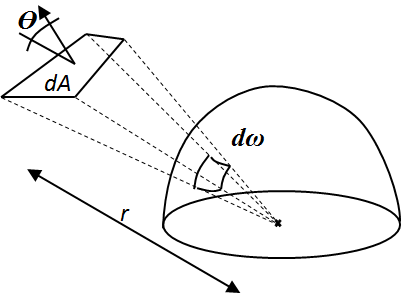
Adott ponthoz képest a térben elhelyezkedő felületdarab nagyságát jellemezhetjük az adott pont köré képzelt egységgömb egy részével, azzal a résszel, ami pontosan eltakarja a felületdarabot a középpontból nézve. Ezt számszerűsíthetjük is (3.32. ábra). Az ábrán dA-val jelölt felületdarab normálisa és a gömb középpontjából húzott sugár bezárt szöge ϴ. Ha a felületdarab középpontja r távolságra van az egységgömb középpontjától, akkor a dω térszög [3.6.] .
|
|
(3.113) |
hiszen a dA felületdarab csak dAcosϴ nagyságot mutat a középpont felé, és a gömb felülete sugarának négyzetével (r 2 -tel) arányos. A térszög mértékegysége a m2/m2=1, a szteradián. A szteradián a radián térbeli általánosítása.
A térszöggel már definiálhatjuk a fénysűrűséget, vagy radianciát. A radiancia a fluxus a felület és a térszög szerinti vegyes deriváltja osztva a az aktuális felületdarab ϴ cosinus-ával.
|
|
(3.114) |
Mértékegysége Watt/m2/sr.
3.5.2. Fényforrások
Ahhoz, hogy megvilágított objektumokat rajzoljunk először a megvilágítást kell modelleznünk.
3.5.2.1. Pontszerű fényforrás (Point Light)
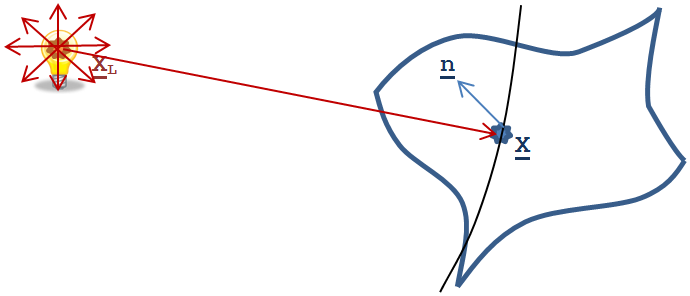
A pontszerű fényforrásnek nincs kiterjedése, és minden irányban azonos fényáramot sugároz. A led fényforrások, a villanykörték a fény forrásától elég távolról vizsgálva pontszerűnek tekinthetők. Egy térben elhelyezett ponttal (xL) modellezhetjük ezeket. Legyen egy felületünk, melynek a megvilágított x pontját vizsgáljuk (3.33. ábra). Világos, hogy a pontszerű fényforrásból kiinduló energia annál kisebb hányada jut a vizsgát felületre, minél messzebb van a felület. Mivel a sugárzott energia a fényforrás középpontú gömb felületén halad keresztül, a gömb egy felületdarabjára jutó energia a gömb felületével fordított arányban csökken, a gömbfelület pedig a sugár (r) négyzetével arányos. Ha azt is figyelembe vesszük, hogy nincs igazi fényforrás, akkor azt mondhatjuk, hogy a felületre jutó energia az r=|x-xL| (3.33. ábra) sugár másodfokú polinomjával fordítottan arányos. Az x pontban a fényáram tehát
|
|
(3.115) |
ahol a, b és c paraméterek megválaszthatók a modellezés során. Ha a fénysugár irányát is figyelembe vesszük, akkor azt mondhatjuk, hogy a felületi pont megvilágítása, mint vektormennyiség (I)
|
|
(3.116) |
A felületdarab megvilágításának erőssége x pontban (L(x)) függ attól is, hogy a beérkező fénysugarak milyen szöget zárnak be az adott pontban értelmezett normálissal (n).
|
|
(3.117) |
3.5.2.2. Irány (párhuzamos) fényforrás (Direction Light)
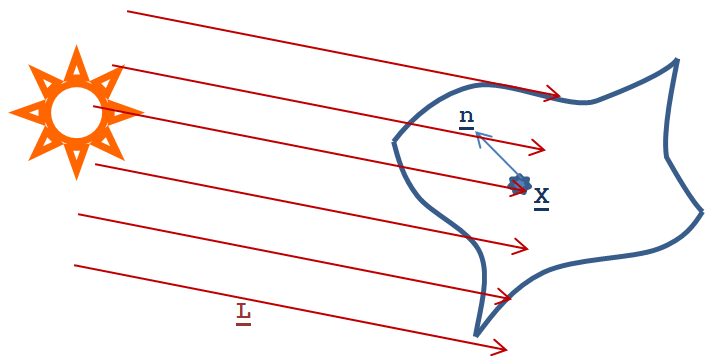
Ha egy nagyon távoli pontot képzelünk el (vagy egy nagyon távoli sugárzó testet, mint a Nap), akkor azt úgy modellezhetjük, hogy a megvilágított felület környékén a fényáram konstans (i). Van azonban iránya, ami nem más, mint a végtelen távoli pont iránya, amely megegyezik a beeső fénysugarak L irányvektorával. A fényáram tehát irányfüggő i( L ).
|
|
(3.118) |
Ezt is ábrázolhatjuk irányfüggő vektormennyiségként (a 3.34. ábra alapján I(L), ahol I iránya megegyezik az L iránnyal, a fényáram pedig i.)
|
|
(3.119) |
Az előzőkhöz hasonlóan a felületdarab megvilágítása x környékén
|
|
(3.120) |
3.5.2.3. Ambiens fényforrás (Ambient Light)
Az ambiens fény egy olyan modellje a szórt fénnyel történő megvilágításnak, ahol minden pontot, minden irányból azonos fényárammal és színnel világítunk meg (3.35. ábra).
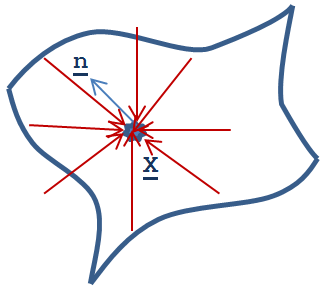
Ezt a modellt arra használjuk, hogy a modellezett objektumok kapjanak egy alap megvilágítást. A felület minden pontjában a fényáram tehát állandó.
|
|
(3.121) |
Ebben az esetben a pontok megvilágításának erőssége, mivel nem függ sem a helytől, sem az iránytól
|
|
(3.122) |
3.5.2.4. Égboltfény (Sky Light)
Az irány fényforrás jellegzetessége a konstans fényáram, párhuzamos sugarakból álló megvilágítás, mint a napfény. Az égboltot is a napfény világítja meg, azonban felhők és épületek árnyékot vethetnek, azaz a különböző területeken más és más állandó párhuzamos fény világít (3.36. ábra).
|
|
(3.123) |
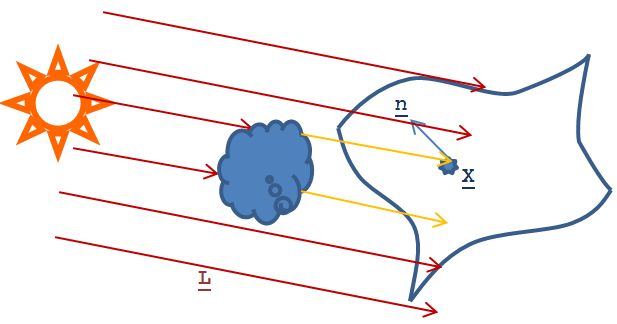
Hasonlóan az irányfényhez az égboltfény is vektormennyiséggel ábrázolható I(L,x), ahol I iránya megegyezik az L iránnyal, a fényáram pedig x-től függ.
|
|
(3.124) |
Az előzőkhöz hasonlóan a felületdarab megvilágítása x környékén
|
|
(3.125) |
3.5.2.5. Reflektorfény (Spot Light)
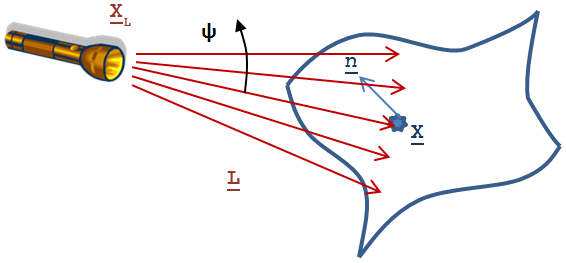
A gépkocsik reflektora vagy az elemlámpák fénycsóvája modellezhető, mint egy pontszerű fényforrás (3.5.2.1. szakasz) fénysugarai, lehatárolva egy parabolikus vagy kúpos tükörrel. A fényforrás sugarai nem tudják megkerülni a tükröt, és a fényáram a fényforrás tengelyétől távolodva (a 3.37. ábra ábrán szög) csökken
|
|
(3.126) |
(3.126) egyenletben r=||x-xL||, m egész szám az a(α) a ψ–nek ablakfüggvénye (ha a szög kisebb, mint ψ, akkor a függvényérték 1, egyébként 0)
|
|
(3.127) |
Ugyanúgy, mint a pontszerű fényforrásoknál a fényáram vektormennyiség.
|
|
(3.128) |
Figyelembe véve a felületi normálist n.
|
|
(3.129) |
3.5.3. Anyagok, visszaverődés
A különböző anyagok tükrözik, szétszórva visszaverik, megtörik vagy elnyelik a fénysugarakat. Az anyagok ilyen viselkedését modellezhetjük a kétirányú visszaverődés-eloszlás függvénnyel. Ennek angol rövidítése a BRDF (Bidirectional Reflection Distribution Function).
3.5.3.1. A BRDF
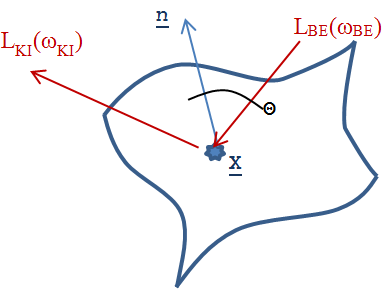
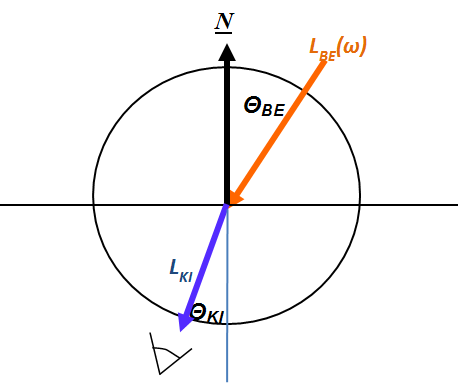
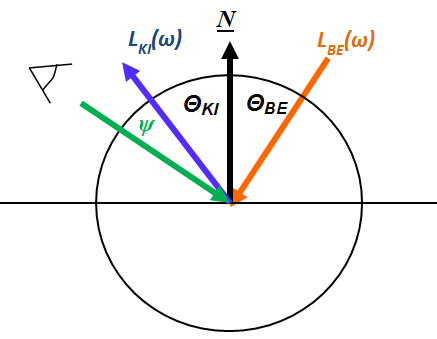
Ha egy felület x pontjába a tér egy ω BE irányából érkezik egy adott hullámhosszú fénysugár, akkor a felületi ω KI irányból szemlélve a két fényáram segítségével definiálhatunk egy, az ω BE , ω KI és x változóktól függő függvényt. Nicodemus definiálta [3.10.] .
|
|
(3.130) |
ahol az ω BE a beeső térszög, az ω KI a kilépő térszög, L BE a belépő, L KI a kilépő fényáram, n a felület normálisa a visszaverődés helyén, Θ pedig a felületi normális és a belépő fénysugár szöge (3.38. ábra).
Ha a (3.130) egyenletben átrendezünk és integrálunk, akkor azt kapjuk, hogy
|
|
(3.131) |
azaz egy pontból kilépő intenzitás egy összeg. Összegezni kell a pontba belépő összes fényáram-értéket szorozva az f r BRDF értékkel és a beeső sugarak beesési merőlegessel bezárt szögének koszinuszával.
A fizikai tartalom miatt a BRDF nem negatív. A visszaverődés nem vonhat el fényt a szemlélőtől.
|
|
(3.132) |
Szintén a fizikai tartalom miatt a
|
|
(3.133) |
hiszen a passzív anyag nem termelhet fényt. A (3.133) egyenletben az integrál kifejezést albedónak hívjuk. Ez viszont azt jelenti, hogy a (3.133) integrandusa éppen egy eloszlásfüggvény. Innen ered a BRDF elnevezés is. Így a (3.134) kifejezés éppen azt a valószínűséget definiálja, hogy a ω
BE
irányból érkező sugár az ω
KI
irány körül dω térszögben távozik
[3.6.]
. Jelölje ω
KI
irány körül dω átmérőjű környezetét 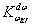 !
!
|
|
(3.134) |
A BRDF értékére fennáll a Helmholz-féle szimmetria összefüggés [3.11.] , mely azt mondja ki, hogy a BRDF kifejezésben a fénysugár iránya megváltoztatható (3.134).
|
|
(3.135) |
Ha a (3.131) egyenletet egyetlen fénysugárra vizsgáljuk, eltekintünk a teljes Ω téren történő integrálástól akkor azt kapjuk, hogy
|
|
(3.136) |
Ha (3.136)-ból kifejezzük a BRDF értéket, akkor az egyszerűsített, egyetlen sugárra vonatkozó BRDF értéket kapjuk.
|
|
(3.137) |
Az egyszerűsített DRDF definíciót használva megvizsgáljuk a különböző diffúz, tükröződő, fénytörő és spekulárisan tükröződő anyagok tulajdonságainak modellezését.
3.5.3.2. Diffúz anyagok jellemzése
A fal például diffúz módon veri vissza a fényt. Ennek lényege, hogy a beérkező, adott hullámhosszú fénysugár esetén minden irányban egyforma fényáram távozik. Az, hogy mi mennyire látjuk a falat világosnak, az csak attól függ, hogy honnan világítjuk meg. A Lambert-törvény írja le a fal, mint diffúz felület megvilágítás hatására történő viselkedését. Legyen megvilágítva a fal ω-irányból I BE (λ) fényárammal. Bárhonnan szemlélve a felületet az I KI (λ) fényáram csak a megvilágítás irányától és az anyag hullámhossztól függő k(λ) jellemzőjétől függ.
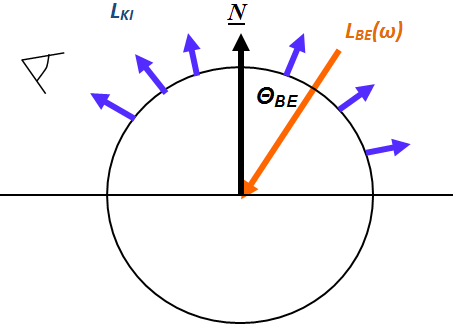
A Lambert-törvény tehát
|
|
(3.138) |
Ha a (3.138) Lambert-törvényt összevetjük a (3.136) egyszerűsített egyenlettel, akkor azt kapjuk, hogy a diffúz felületek BRDF kifejezése adott hullámhosszon csak a fény hullámhosszától függ.
|
|
(3.139) |
3.5.3.3. Reflexív anyagok, ideális visszaverődés
Ha egy tükröt egy fénysugárral megvilágítunk, a tükör azt a fénysugarat úgy veri vissza, hogy a visszavert sugár benne fekszik a beeső fény és a beesési merőleges által meghatározott síkban és ugyanakkora szöget zár be a beesési merőlegessel, mint a bejövő fénysugár. A fenti viselkedést formalizálhatjuk a Lambert-törvény (3.138) megfogalmazásának megfelelően,
|
|
(3.140) |
ahol a 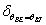 szimbólum a Kronecker-szimbólum, azaz
szimbólum a Kronecker-szimbólum, azaz
|
|
(3.141) |
A (3.140) kifejezést összevetve (3.136)-tal, adódik, hogy a tükrös felület esetén a BRDF
|
|
(3.142) |
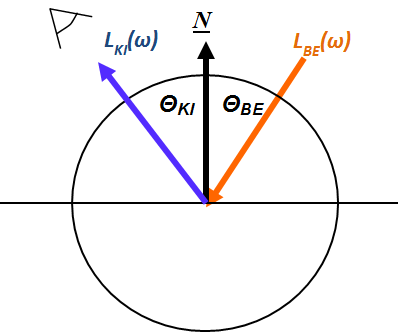
A (3.142) kifejezésben a  a tükröződő anyag Fresnel-együtthatója, azt adja meg, hogy a tükör a beeső fényáram hanyadrészét veri vissza
[3.5.]
.
a tükröződő anyag Fresnel-együtthatója, azt adja meg, hogy a tükör a beeső fényáram hanyadrészét veri vissza
[3.5.]
.
3.5.3.4. Ideális törés
A fénytörésről szóló Snellius-Descartes-törvény [3.12.] szerint a beeső fénysugár, a beesési merőleges és a megtört fénysugár egy síkban helyzkednek el. A merőlegesen beeső fénysugár nem törik meg. Végül a beesési szög (α) szinuszának és a törési szög (β) szinuszának aránya a közegekben mért terjedési sebességek (c 1 ,c 2 ) arányával egyenlő, ami megegyezik a két közeg relatív törésmutatójával (n 2 /n 1 =n 2,1 ). Lásd 3.41. ábra.
|
|
(3.143) |
Ebben az esetben a Lambert-törvényhez hasonlóan formalizálva a (3.140)-t írhatjuk, hogy
|
|
(3.144) |
illetve
|
|
(3.145) |
3.5.3.5. Phong illuminácós modell
A fényvisszaverő anyagok általában sem tisztán diffúz módon (3.5.4.2. szakasz fejezet), sem tisztán reflexív módon (3.5.4.3. szakasz fejezet) verik vissza a fényt, hanem a kettő között valahogy. Az ilyen felületeket spekuláris felületeknek nevezzük, és a visszaverődés leírása Phong nevéhez köthető. Phong modellje szerint a visszaverődés nagy része az elméleti visszaverődés irányában és annak környezetében történik [3.12.] .
|
|
(3.146) |
Ahol a ψ szög az elméleti visszaverődési irány és a ránézés szöge közt mérhető szög.
Ennek alapján a BRDF Phong-modell esetén.
|
|
(3.147) |
3.5.4. Az árnyalás modellezése
Ha az árnyalást modellezni akarjuk, nagyon nehéz feladatunk van, hiszen egy test megvilágítása függ a környezetétől, azonban a test hatással van a környezetésre is.
3.5.4.1. Az árnyalási egyenlet
Ha a BRDF (3.130) definícióját kibővítjük azzal, hogy a térben még fénykibocsátó pontok is lehetnek (LE), valamint a teljes reflexió függ a λ hullámhossztól és a t időtől, akkor a szembe érkező fényáram valamint a f BRDF akármilyen lehet a fenti modellek közül az adott pontban
|
|
(3.148) |
A (3.148) egyenletet szokás árnyalási egyenletnek nevezni. Mivel az integrálegyenlet mindkét oldalán szerepel az ismeretlen L() függvény, ennek csak egyszerűsítések melletti numerikus megoldása lehetséges [3.6.] . Most csak egy egészen egyszerű közelítéssel, a sugárkövetéssel és az úgynevezett lokális illuminációval foglalkozunk.
3.5.4.2. Sugárkövetés
Ha a képernyő pixeleire egyenként, a fényforrásokból kiinduló, pixelen átmenő fénysugarak útját a fényforrásokból kiindulva az objektumok – a 3.5.4. szakasz fejezetben leírtaknak megfelelően – modelljén megtörve vagy áthaladva vizsgáljuk, azt sugárkövetéses módszernek hívjuk. Mivel egy fényforrásból is végtelen sok irányban indulhat fénysugár, ez még diszkrét közelítéssel is, követve egészen a képig, vagy a vizsgált térből való kilépésig, kizárja a valós idejű szimulációt.
A fordított sugárkövetés esetén a kép pontjainak meghatározásához a fény haladásával ellenkező irányban járhatjuk végig a fény útját, a képernyőtől a fényforrásokig haladva. Csak azokat a fénysugarakat vesszük figyelembe, amelyek a fényforráshoz érnek.
3.5.4.3. Inkrementális képszintézis, egyszerűsített árnyalási egyenlet
Sokkal egyszerűbb kifejezést kapunk, ha eltekintünk a hullámhossztól és az időtől való függéstől. Elhagyunk még a (3.148) egyenletből minden csatolást (a jobb és bal oldalon is szerepel a fényáram, illetve, hogy egy objektum megvilágítása saját visszavert fényétől is függ). Feltételezzük azt is, hogy a képen látható felületekre csak a fényforrásokból közvetlen módon érkezik fény, csak az l darab fényforrásra kell összegezni az adott felületpontba érkező fénysugarakat, és azokat az f BRDF-fel figyelembe venni. A (3.149) képletben szerepel egy úgynevezett ambiens fény, amivel a nem figyelembe vett térbeli megvilágításokat kompenzálhatjuk (L A ). Ennek a felület k A -szorosát veri vissza minden irányba [3.6.] .
|
|
(3.149) |
3.5.4.4. Felületek közelítő árnyalása
Ha az egyszerűsített árnyalási egyenlettel is számítjuk a felület pontjainak megjelenését, akkor is a felületeknek végtelen sok pontjuk van, így ez is megoldhatatlan feladat. Ha az árnyalást csak a felületek bizonyos pontjaiban számítjuk ki, és a köztes pontban a felület színét, fényességét a kiszámított pontok alapján interpoláljuk, akkor eredményre jutunk. A Gouraud-árnyalás a felületeket háromszögekkel közelíti, és a háromszögek csúcsaiban számítja csak a pontok megjelenését. A háromszögeken belül lineáris interpolációval számítjuk a megjelenést a sarokpontok alapján.
A Phong-féle árnyalás szintén a háromszögek sarokpontjaiból indul ki, a sarokpontokban kiszámítja a normálvektort, és feltételezi, hogy a belső pontokban a normálvektor a sarokpontok normálvektorainak interpolációjából számítható.
3.5.4.5. Fénysugarak haladása nem átlátszó térben
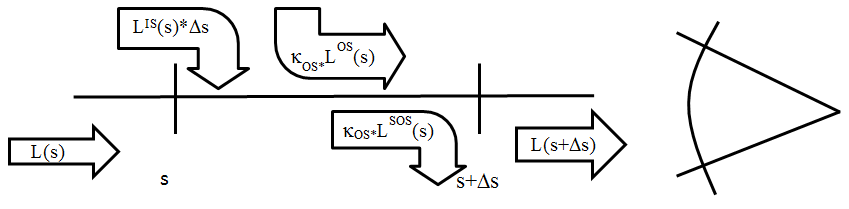
Tegyük fel, hogy az egyenes vonalban haladó L(s) fényáram haladási irányában valós fényelnyelő közegen (például poros levegő, felhő köd) halad át, míg a szemünkhöz ér, vagy a fény egy fénykibocsátó anyagon (ilyen például a tűz) halad át, illetve más irányból érkező fényáramok is folytathatják útjukat a vizsgált irányban. Ezekben az esetekben a 3.43. ábra szerint egy Δs útszakaszon megváltozik a fényáram, L(s+Δs) lesz.
A fény megtörhet a fényelnyelő anyagon, és a Δs útszakaszon ezt az egy egységnyi hosszon történő κ os fényáram-szórási tényezővel vehetjük figyelembe, így a fényáram κ os *L(s)*Δs értékkel csökken.
Ha a fénykibocsátó anyagon keresztül vezet, aminek önálló fényárama a kérdéses irányban L e , akkor ezt egységnyi hosszon κ E tényezővel figyelembe véve a fényáram κ E *L E *Δs értékkel nő.
Ha más irányból érkező, a fényszóró anyagon megtört fénysugár a vizsgált irányban folytatja az útját, akkor az a Δs hosszon L IS (s)* Δs értékű fényáram-növekedést okoz.
Ha felírjuk a fényáramot az s és az s+Δs pontokban, akkor
|
|
(3.150) |
azaz, ha Δs minden határon túl csökken, akkor
|
|
(3.151) |
Természetesen a (3.151) egyenlet csak akkor oldható meg egyszerűen ha L IS független L-től, és csak egyetlen irányt vizsgálunk, egyébként csak tovább bonyolítottuk a (3.149) árnyalási egyenletet.
Irodalmak:
[3.1.] Bevezetés a geometriába. Tankönyvkiadó . Budapest . 1960.
[3.2.] Differenciálgeometria. Műszaki Könyvkiadó . Budapest . 1979.
[3.3.] Numerikus módszerek I.. Typotex kiadó. Budapest . 2002.
[3.4.] Numerikus analízis. Tankönyvkiadó . Budapest . 1978.
[3.5.] „A Variational Approach to Spline Functions Theory,”. Rend. Sem. Mat. Univ. Pol. Torino. p. 3.. 2003.
[3.6.] Háromdimenziós Grafika, animáció és játékfejlesztés. ComputerBooks . Budapest . 2003.
[3.7.] A Practical Guide to Splines. Springer-Verlag . München . 1978.
[3.8.] „Komputergrafika – Matematikai alapok,” [Online]. Available: http://www.inf.unideb.hu/kmitt/konvkmitt/komputergrafika_matematikai_alapok/book.xml.html.. Hozzáférés dátuma: 2013.
[3.9.] Silicon Graphics „www.sgi.com"[Online]. 2012.
[3.10.] Reflectance Nomenclature and Directional Reflectance and Emissivity. Appl. Optics. pp. 1474-1475.. 1970.
[3.11.] Theory of Reflectance and Emittance Spectroscopy. Cambridge: University Press. Cambridge UK . 1993.
[3.12.] Advanced Animation and Rendering Techniques: Theory and Practice. Addison-Wesley Professional . . 1992.