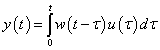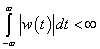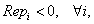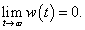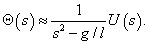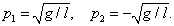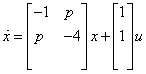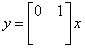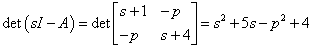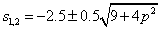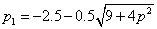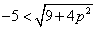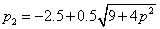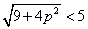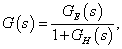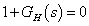5. fejezet - Stabilitásvizsgálat
5.1. Rendszer stabilitása
Tekintsünk egy lineáris időinvariáns dinamikus rendszert, amelynek bemenőjele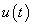 
, 
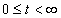, kimenőjele pedig 
, 
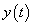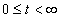. Adott a rendszer 
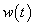súlyfüggvénye, illetve ennek 
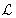-transzformáltja: 
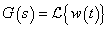. A bemenet/kimenet kapcsolatot zérus kezdeti feltétele mellett az alábbi konvolúciós integrál adja meg:
|
|
(234) |
Feltettük, hogy a rendszer a kezdeti időpontban nyugalmi állapotban van. Ezután feltehetjük a kérdést, hogy mi a feltétele annak, hogy ha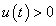 
gerjesztés éri a rendszert, és az 
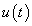valamilyen tulajdonsággal rendelkezik, milyen feltételek esetén rendelkezik a kimenőjel is ugyanilyen tulajdonsággal.
Tétel 4.1 Egy lineáris időinvariáns dinamikus rendszer stabilis akkor és csak akkor, ha
(a) A rendszer súlyfüggvénye abszolút integrálható,
|
|
(235) |
(b) A rendszer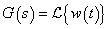 
átviteli függvényének pólusai a baloldali komplex félsíkon helyezkednek el, azaz
|
|
(236) |
ahol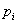 
a 
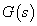pólusa.
(c) A súlyfüggvény határértéke zérus, azaz
|
|
(237) |
Példa 4.1
Az inverz inga egy
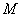tömegű kocsira rögzített csapágyon szabadon elforgó rúd, amelynek
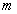tömege a rúd felső végére van redukálva.
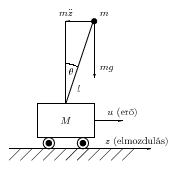
A feladat megoldása: A rúd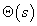 
szögelfordulása a következőképpen függ az 
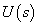gerjesztő erőtől:
|
|
(238) |
Az átviteli függvény pólusai:
|
|
(239) |
A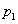 
pólus a jobboldali komplex félsíkra esik, tehát az inverz inga labilis.
Példa 4.2
A p paraméter milyen értékei esetén lesz stabil az alábbi állapottér reprezentáció:
|
|
(240) |
|
|
(241) |
A feladat megoldása:
|
|
(242) |
|
|
(243) |
Stabil, ha mindkét pólus negatív valós értékű.
|
|
(244) |
|
|
(245) |
ami mindig teljesül, azaz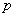 
bármely értékére 
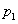negatív értékű.
1. eset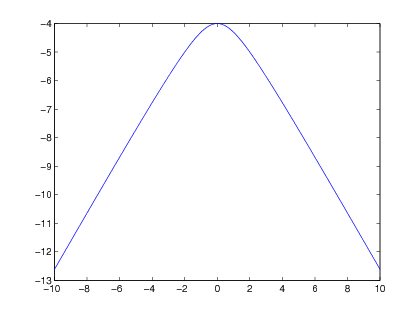
2. eset
|
|
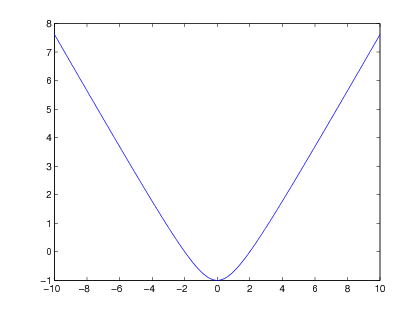
(246) |
|
|
(247) |
A negatív valós érték feltétele, hogy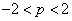 
legyen.
5.1.1. Zárt rendszer stabilitása
A szabályozó tervezésénél mindig biztosítani kell, hogy akár stabilis, akár labilis a szabályozott folyamat, a zárt rendszer stabilis legyen. A zárt rendszer átviteli függvénye:
|
|
(248) |
ahol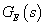 
az előrevezető ág átviteli függvénye és 
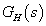a hurokátviteli függvény.
A zárt rendszer stabilis akkor és csak akkor, ha pólusai a baloldali komplex számsíkon helyezkednek el, tehát az
|
|
(249) |
egyenlet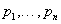 
gyökereire teljesül a 
, 
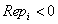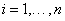feltétel, ahol 
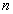a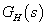 
pólusainak száma.
A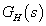 
a hurokátviteli függvény pólusai alapján vizsgálhatjuk a zárt rendszer stabilitását. Pólusok és a stabilitás kapcsolata:
- ha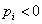 
, akkor a zárt rendszer stabilis,
- ha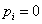 
, határeset,
- ha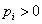 
, akkor a zárt rendszer labilis,
ahol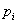 
a zárt rendszer pólusa.
A Nyquist szabályozási kritérium a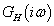 
hurokátviteli frekvencia függvény alapján képes a zárt rendszer stabilitásáról képet adni.
Rajzoljuk meg a frekvencia függvényt a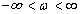 
tartományra. A negatív frekvenciákra a függvény a pozitív frekvenciákra ismert függvénynek a valós tengelyre vett tükörképe lesz.
Tétel 4.2 (Nyquist kritérium)
Ha a
(
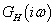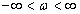) felnyitott hurok frekvencia függvénye a növekvő frekvenciák irányába haladva
- nem veszi körül a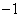 
pontot, akkor a rendszer stabilis,
- átmegy a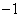 
ponton, akkor a rendszer a stabilitás határán van,
- körülveszi a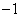 
pontot, akkor a rendszer labilis.
Ha a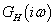 
frekvencia függvény a növekvő frekvenciák irányába haladva nem veszi körül a 
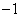pontot, akkor a zárt rendszer rendszer stabilis. Ha a 
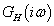frekvencia függvény épp átmegy a komplex számsík 
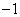pontján, akkor a 
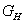frekvencia függvénynek 
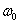körfrekvencián a zárt rendszerben csillapítatlan lengések keletkeznek. Ekkor a zárt rendszer a stabilitás határán van.
5.1.2. Bode-stabilitási kritérium
A stabilitás analízist a Bode diagram alapján is elvégezhetjük, ezek az ún. Bode-stabilitási kritériumok.
- Ha -20 dB/dek-dal metszi a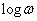 
tengelyt, akkor a zárt rendszer stabilis.
- Ha -40 dB/dek-dal metszi a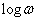 
tengelyt, akkor a vágási frekvencián érvényes fázisszög értéke dönt a zárt rendszer stabilitásáról. Ha 
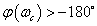, akkor a zárt rendszer stabilis, míg ha 
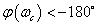, akkor a zárt rendszer labilis.
- Ha -60 dB/dek-dal metszi a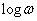 
tengelyt, akkor a zárt rendszer labilis.
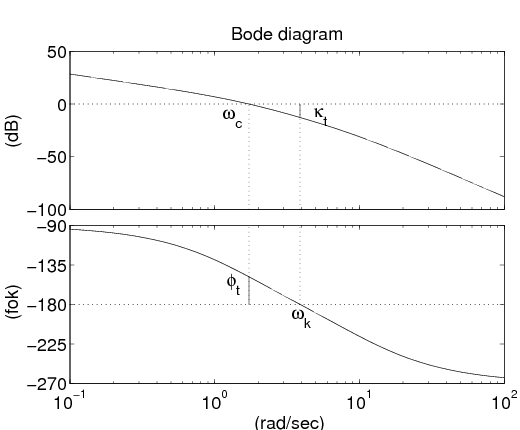
A zárt szabályozási körök stabilitásával kapcsolatban bevezetjük a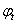 
fázistartalék fogalmát: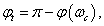 
- Ha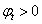 
, akkor a zárt rendszer stabilis.
- Ha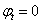 
, határeset.
- Ha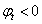 
, akkor a zárt rendszer labilis.
A zárt szabályozási körök stabilitásával kapcsolatban bevezetjük a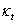 
erősítési tartalék fogalmát. Azt mutatja, hogy mennyivel tudjuk még növelni a statikus körerősítést, úgy, hogy épp a stabilitás határára kerüljön a rendszer. Erősítési tartalék és a stabilitás kapcsolata:
- Ha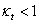 
, akkor a zárt rendszer stabilis.
- Ha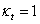 
, határeset.
- Ha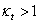 
, akkor a zárt rendszer labilis.