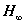13. fejezet - Hinf. szabályozók tervezése
Vissza		Előre

13. fejezet - Hinf. szabályozók tervezése

Tartalom

13.1. Véges horizontú FI feladat
13.2. Végtelen horizontú FI feladat
13.3. A OE feladat
13.4. Egyszerűsített kimenet visszacsatolásos feladat

Bár az egyszerüsített kimenet-visszacsatolásos optimális $ℋ_{\infty}$ szabályozó kiszámítása jórészt az optimális $ℋ_{2}$ szabályozó levezetésénél alkalmazott lépéseket követi, vannak lényegi tulajdonságok, amik megkülönböztetik a két esetet.

Egyrészt nyilvánvaló, hogy egy stabil lineáris $P$ rendszerre es egy adott $γ > 0$ esetén $∥ P ∥_{\infty} < γ$ akkor es csak akkor, ha létezik $ε > 0$ amellyel

$∥ z ∥_{2}^{2} - γ^{2} ∥ w ∥_{2}^{2} \leq - ε ∥ w ∥_{2}^{2}$

(594)

minden $w \in ℒ_{2}$ jelre. Ezt a feltételt átírhatjuk

$- ε ∥ w ∥_{2}^{2} > \int_{0}^{\infty} z^{T} z d t - γ^{2} \int_{0}^{\infty} w^{T} w d t = lim_{T \to \infty} \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t,$

(595)

alakba, ami azt sugallja, hogy lehetséges egy véges horizontú szabályozót definiálni, ami határesetben, ahogy a $T$ tart végtelenhez, megközelíti a $ℋ_{\infty}$ szabályozót. Így, mint azt a $ℋ_{2}$ esetben tettük, először célszerű a véges-horizontú FI feladatot megvizsgálni, ahol a költségfüggvény

$J (u, w, T, Ψ) = \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t + x^{T} (T) Ψ x (T)$

(596)

alakú, ahol $Ψ > 0$ es $w \in ℒ_{2}$ .

Kimutatható, hogy ennek a feladatnak a megoldása egy $K_{T}$ szabályozó, ami egy olyan $u_{*, T}$ irányító bemenetet generál, amelyre létezik $ε > 0$ úgy, hogy

$J (u_{*, T}, w, T, Ψ) < - ε ∥ w ∥_{2, [0, T]}^{2}$

(597)

fennáljon minden $w \in ℒ_{2, [0, T]}$ esetén, vagyis $∥ ℱ_{ℓ} (P, K_{T}) ∥_{[0, T]} \leq γ$ . Határesetben azt várjuk, hogy

$∥ ℱ_{ℓ} (P, K_{T}) ∥_{[0, T]} \to ∥ ℱ_{ℓ} P, K) ∥_{\infty} < γ .$

(598)

Azonban az optimális $ℋ_{2}$ feladattal szemben az optimális $ℋ_{\infty}$ irányítástervezésnek nem minig van megoldása, ha $γ$ túl kicsi, a zavaró $- γ^{2} w^{T} w$ tag jelenléte miatt a költségfüggvényben. Tekinthetjük úgy, hogy az optimalizálási feladat megoldása egy olyan játszma kimenetele, amelyben a szabályozó célja egy, a költséget minimalizáló $u$ irányító bemenet tervezése, míg a környezet egy olyan $w$ zavarással hat ami maximalizálja ezt a költséget.

Tehát a $J (u, w, T, Ψ)$ költség függvénye $u$ -nak és $w$ -nek. Ha a zavarási stratégia adott akkor $J (u, w, T, Ψ)$ egy konvex függvény aminek globális minimuma az $u_{*, T}$ irányításra vétetik fel, amit az optimális $K_{*, T}$ szabályozó general. Ha az irányítás fix és a $w$ környezeti hatás változik akkor a $J (u, w, T, Ψ)$ egy konkáv funkcionál, aminek aminek globális maximuma $w_{*}$ esetén adódik.

A két játékos optimális stratégiája a nyeregpontban van, vagyis a költségfüggvény inflexiós pontjában, ahol a szabályozó a lehető legjobb irányítást alkalmazza a legrosszabb szavarás feltételezése mellett.

Legyen $(u_{*}, w_{*})$ ez a nyeregponti stratégia, amit az alábbi feltétel jellemez:

$J (u_{*}, w, T, Ψ) \leq J (u_{*}, w_{*}, T, Ψ) \leq J (u, w_{*}, T, Ψ) .$

(599)

Tehát a $ℋ_{\infty}$ optimális eljárás a legrosszabb esetre készül fel, ami egy konkrét zavarás esetén nem feltétlenül adja az arra a zavarásra optimális választ.

13.1. Véges horizontú FI feladat

A véges horizontú FI feladat a

$J (u, w, T, Ψ) = \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t + x^{T} (T) Ψ x (T)$

(600)

költségfüggvény $(u_{*, T}, w_{*, T})$ nyeregponti stratégiáját keresi, ahol a rendszer az alábbi formában adott:

$P_{F I} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & 0 & D_{12} \\ I & 0 & 0 \\ 0 & I & 0 \end{array}] .$

(601)

A továbbiakban feltételezzük, hogy létezik ilyen $(u_{*, T}, w_{*, T})$ nyeregpont.

Elöször rögzítsük $w = w_{*, T}$ -t és tekintsük $u = u_{*, T} + η \tilde{u}$ jelet, ahol $η$ egy kis állandó. Jelölje $x^{*}$ a nyeregponti trajektóriát, vagyis

${\dot{x}}^{*} = A x^{*} + B_{1} w_{*, T} + B_{2} u_{*, T}, x^{*} (0) = 0,$

(602)

és legyen $x$ az $u$ által meghatározott trajektória, vagyis

$\dot{x} = A x + B_{1} w_{*, T} + B_{2} u, x (0) = 0.$

(603)

Következik, hogy $x = x^{*} + η \tilde{x}$ ahol $\tilde{x}$ kielégíti a

$\frac{d}{d t} \tilde{x} = A \tilde{x} + B_{2} \tilde{u}, \tilde{x} (0) = 0$

(604)

egyenletet, azaz $\tilde{x} (t) = \int_{0}^{T} Φ (t, τ) B_{2} \tilde{u} d τ$ ahol $Φ (t, τ)$ az $A$ -nak megfelelő alapmátrix.

Ekkor a perturbált költségfüggvény alakja

$J (u, w_{*, T}, T, Ψ) = \int_{0}^{T} (x^{*} C_{1}^{T} C_{1} x^{*} + u_{*, T}^{T} u_{*, T} - γ^{2} w_{*, T}^{T} w_{*, T}) d t +$

$+ {(x^{*})}^{T} (T) Ψ x^{*} (T) + 2 η {\int_{0}^{T} ({\tilde{x}}^{T} C_{1}^{T} C_{1} x^{*} + {\tilde{u}}^{T} u_{*, T}) d t + {\tilde{x}}^{T} (T) Ψ x^{*} (T)} +$

$+ η^{2} {\int_{0}^{T} ({\tilde{x}}^{T} C_{1}^{T} C_{1} \tilde{x} + {\tilde{u}}^{T} \tilde{u}) d t + {\tilde{x}}^{T} (T) Ψ \tilde{x} (T)} .$

(605)

Mivel az első tag $J (u_{*, T}, w_{*, T}, T, Ψ)$ és

$J (u, w_{*, T}, T, Ψ) \geq J (u_{*, T}, w_{*, T}, T, Ψ)$

(606)

következik, hogy

$0 \leq J (u, w_{*, T}, T, Ψ) - J (u_{*, T}, w_{*, T}, T, Ψ) = 2 η {\int_{0}^{T} ({\tilde{x}}^{T} C_{1}^{T} C_{1} x^{*} + {\tilde{u}}^{T} u_{*, T}) d t +$

$+ {\tilde{x}}^{T} (T) Ψ x^{*} (T)} + η^{2} {\int_{0}^{T} ({\tilde{x}}^{T} C_{1}^{T} C_{1} \tilde{x} + {\tilde{u}}^{T} \tilde{u}) d t + {\tilde{x}}^{T} (T) Ψ \tilde{x} (T)} .$

(607)

Elég kis $| η |$ esetén a jobboldal negatív. Mivel $J (u, w_{*, T}, T, Ψ) \geq 0$ adódik, hogy

$\int_{0}^{T} {{\tilde{x}}^{T} C_{1}^{T} C_{1} x^{*} + {\tilde{u}}^{T} u_{*, T}) d t + {\tilde{x}}^{T} (T) Ψ x^{*} (T) = 0.$

(608)

Bevezetve az alábbi társváltozót

$λ (t) = \int_{t}^{T} Φ^{T} (τ, t) C_{1}^{T} C_{1} x^{*} d τ + Φ^{T} (T, t) Ψ x^{*} (T),$

(609)

minden $\tilde{u}$ -ra, a következő feltétel adódik:

$\int_{0}^{T} \tilde{u} (B_{2}^{T} λ (t) + u_{*, T} (t)) d t = 0,$

(610)

azaz a nyeregponti optimális irényítás

$u_{*, T} = - B_{2}^{T} λ (t),$

(611)

ahol $t \leq T$ .

A fenti gondolatmenetet megismételhetjük, hogy a legrosszabb $w_{*, T}$ zavarás egy jellemzését megkapjuk: rögzítsük $u = u_{*, T}$ -t és $w = w_{*, T} + η \tilde{w}$ ahol $0 \leq t \leq T$ . A perturbáló jel egy tetszőleges $ℒ_{2} [0, T]$ -beli függvény és $η$ egy tetszőleges állandó.

Eza perturbáció egy $x = x^{*} + η \tilde{x}$ trajektórát generál, ahol $0 \leq t \leq T$ és $\tilde{x}$ kielégíti az

$\frac{d}{d t} \tilde{x} = A \tilde{x} + B_{1} \tilde{w}, \tilde{x} (0) = 0,$

(612)

egyenletet, azaz $\tilde{x} (t) = \int_{0}^{t} Φ (t, τ) B_{1} \tilde{w} d τ$ .

Ezt behelyettesítve $J (u, w, T, Ψ)$ -be kapjuk, hogy

$\int_{0}^{T} {{\tilde{x}}^{T} C_{1}^{T} C_{1} x^{*} - γ^{2} {\tilde{w}}^{T} w_{*, T}) d t + {\tilde{x}}^{T} (T) Ψ x^{*} (T) = 0,$

(613)

vagyis minden $\tilde{w}$ esetén

$\int_{0}^{T} {\tilde{w}}^{T} (B_{1}^{T} λ - γ^{2} w_{*, T}) d t = 0.$

(614)

A társváltozó segítségével a legrosszabb zavarás kifejezhető mint

$w_{*, T} (t) = \frac{1}{γ^{2}} B_{1}^{T} λ (t),$

(615)

ahol $0 \leq t \leq T$ .

Mint ahogyan az optimális LQ irányításnál már láttuk, az optimális állapot és társváltozó kielégíti az alábbi peremérték feladatot:

$\frac{d}{d t} (\begin{array}{l} x^{*} \\ λ \end{array}) = (\begin{array}{l} A & - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) \\ - C_{1}^{T} C_{1} & - A^{T} \end{array}) (\begin{array}{l} x^{*} \\ λ \end{array}),$

(616)

$(\begin{array}{l} x^{*} (0) \\ λ (T) \end{array}) = (\begin{array}{l} 0 \\ Ψ x^{*} (T) \end{array}) .$

(617)

$H = (\begin{array}{l} A & - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) \\ - C_{1}^{T} C_{1} & - A^{T} \end{array})$

(618)

mátrix a rendszerhez rendelt Hamiltonian mátrix. A társváltozó kifejezhető mint

$λ (t) = X (t) x^{*} (t)$

(619)

ahol $X (t)$ egy mátrixértékű függvény. Ekkor az optimális irányítás és a legrosszabb zavarás alakja

$u_{*, T} (t) = - B_{2} X (t) x^{*} (t), w_{*, T} (t) = γ^{- 2} B_{1} X (t) x^{*} (t) .$

(620)

Várakozásunknak megfelelően $X (t)$ megoldása egy mátrix Riccati differenciál egyenletnek:

$- \dot{X} = X A + A^{T} X + X (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X + C_{1}^{T} C_{1}, X (T) = Ψ .$

(621)

Ennek az $X$ -nek a segítségével a költségfüggvény alakja

$J (u, w, T, M) = \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) + \frac{d}{d t} x^{T} X x) d t =$

$= \int_{0}^{T} (x^{T} (C_{1}^{T} C_{1} + A^{T} X + X A + \dot{X}) x + u^{T} u - γ^{2} w^{T} w +$

$+ (w^{T} B_{1} + u^{T} B_{2}^{T}) X x + x^{T} X (B_{1} w + B_{2} u)) d t =$

$= \int_{0}^{T} [x^{T} X (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X x + u^{T} u - γ^{2} w^{T} w +$

$+ (w^{T} B_{1}^{T} + u^{T} B_{2}^{T}) X x + x^{T} X (B_{1} w + B_{2} u)] d t =$

$= \int_{0}^{T} [(x^{T} X B_{2} B_{2}^{T} X x + u^{T} B_{2}^{T} X x + x^{T} X B_{2} u + u^{T} u) -$

$- γ^{2} (w^{T} w - w^{T} B_{1}^{T} X x - x^{T} X B_{2} w + γ^{- 4} x^{T} X B_{1} B_{1}^{T} X x)] d t =$

$= \int_{0}^{T} {(u + B_{2}^{T} X x)}^{T} (u + B_{2} X x) d t -$

$- γ^{2} \int_{0}^{T} {(w - γ^{- 2} B_{1}^{T} X x)}^{T} (w - γ^{- 2} B_{1}^{T} X x) d t =$

$= ∥ u - u_{*, T} ∥_{2, [0, T]}^{2} - γ^{2} ∥ w - w_{*, T} ∥_{2, [0, T]}^{2}$

(622)

formában írható.

Bevezetve azt az $L$ rendszert ami $w$ -t a $w - w_{*, T}$ -be viszi, kapjuk, hogy

$L (s) = [\begin{array}{l} A - B_{2} B_{2}^{T} X & B_{1} \\ - γ^{- 2} B_{1}^{T} X & I \end{array}] .$

(623)

Ezzel következik, hogy

$J (u_{*, T}, w, T, Ψ) = - γ^{2} ∥ w - w_{*, T} ∥_{2, [0, T]}^{2} =$

$- γ^{2} ∥ L w ∥_{2, [0, T]}^{2} \leq - ε ∥ w ∥_{2, [0, T]}^{2}$

(624)

ahol $ε = γ^{2} / ∥ L ∥_{[0, T]}^{2}$ . Így az optimális $K^{*}$ szabályozó kielégíti a

$J (u_{*, T}, w, T, Ψ) < - ε ∥ w ∥_{2}^{2} \leq 0$

(625)

feltételt minden $w \in ℒ_{2} [0, T]$ esetén, azaz bisztosítja, hogy $∥ ℱ_{ℓ} (P, K^{*}) ∥_{[0, T]} \leq γ$ .

13.2. Végtelen horizontú FI feladat

A $ℋ_{2}$ esetben már látott módon a végtelen horizontú optimális irányítás alakja

$u_{*, T} (t) = - B_{2}^{T} X x (t)$

(626)

ahol $X$ a

$X A + A^{T} X - X (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X + C_{1}^{T} C_{1} = 0$

(627)

$ℋ_{\infty}$ algebrai Riccati egyenlet pozitív definit megoldása amire $A - B_{2} B_{2}^{T} X$ aszimptotikusan stabilis.

A $ℋ_{2}$ és $ℋ_{\infty}$ eset közötti különbség az algebrai Riccati egyenlet alakjában nyilvánul meg. Míg a $ℋ_{2}$ Riccati egyenletnek létezik stabilizáló megoldása, ha

(a) $(A, B_{2})$ stablizálható,

(b) $(C_{1}, A)$ párnak nincsenek nem megfigyelhető módusai a képzetes tengelyen,

ez nem elégséges a $ℋ_{\infty}$ Riccati egyenletre. A továbbiakban feltesszük, hogy ezek a szükséges feltételek fennállnak és a

$- \frac{d}{d t} X (t, T) = X A + A^{T} X - X (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X + C_{1}^{T} C_{1}, X (T, T) = X_{2}$

(628)

Riccati differenciál egyenletnek vannak $X (t, T, X_{2})$ megoldásai minden $T$ -re, ahol $X_{2} > 0$ a $ℋ_{2}$ alakú

$X_{2} A + A^{T} X_{2} - X_{2} B_{2} B_{2}^{T} X_{2}^{T} + C_{1}^{T} C_{1} = 0$

(629)

Riccati egyenlet megoldása.

Feltehetjük, hogy a véges horizontú feladatok költségfüggvényei

$J (u, w, T, X_{2}) = \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t + x^{T} (T) X_{2} x (T),$

(630)

alakban írhatók, azaz $X_{2}$ a terminális kültség.

Legyen $x_{0}$ egy tetszőleges nemzérus kezdeti érték és $w$ tetszőleges $ℒ_{2}$ -beli zavarás.Hogy kimutassuk $X (t, T, X_{2})$ egyenletes korlátosságát $T$ -ben, meg kell mutatnunk, hogylétezik $β > 0$ amire $x_{0}^{T} X (t, T, X_{2}) x_{0} < β ∥ x_{0} ∥^{2}$ minden $T > 0$ esetén.

A linearitást felhasználva $z = z_{w} + z_{x_{0}}$ ahol $z_{x_{0}}$ és $z_{w}$ jelöli az $x_{0}$ és $w$ hatását $z$ -re.Mivel a szabályozó stabilizálja a rendszert, létezik $α > 0$ amire $∥ z_{x_{0}} ∥_{2} \leq α ∥ x_{0} ∥$ .Mivel a szabályozó garantálja, hogy $∥ ℱ_{ℓ} (P, K) ∥_{\infty} < γ$ , létezik $ε > 0$ úgy, hogy $∥ z ∥_{2}^{2} - γ^{2} ∥ w ∥_{2}^{2} \leq - ε ∥ w ∥_{2}^{2}$ . Következik, hogy

$∥ z ∥_{2}^{2} - γ ∥ w ∥_{2}^{2} \leq ∥ z_{w} ∥_{2}^{2} - γ^{2} ∥ w ∥_{2}^{2} + ∥ z_{x_{0}} ∥_{2}^{2} + 2 ∥ z_{x_{0}} ∥_{2} ∥ z_{w} ∥_{2} \leq$

$\leq - ε ∥ w ∥_{2}^{2} + α^{2} ∥ x_{0} ∥^{2} + 2 γ α ∥ x_{0} ∥ ∥ w ∥_{2} =$

$= (α^{2} + \frac{γ^{2} α^{2}}{ε}) ∥ x_{0} ∥^{2} - ε {(∥ w ∥_{2} - \frac{γ α}{ε} ∥ x_{0} ∥)}^{2}$

(631)

azaz,

$∥ z ∥_{2}^{2} - γ ∥ w ∥_{2}^{2} \leq (α^{2} + \frac{γ^{2} α^{2}}{ε}) ∥ x_{0} ∥^{2} = β ∥ x_{0} ∥^{2}$

(632)

minden $x_{0}$ és minden $w \in ℒ_{2}$ esetén.

Mivel

$J (u, w, T, X_{2}) = \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t + x^{T} (T) X_{2} x (T) =$

$= \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w + \frac{d}{d t} (x^{T} X x)) d t + x_{0}^{T} X (0, T, X_{2}) x_{0} =$

$= ∥ u - u_{*, T} ∥_{2, [0, T]}^{2} - γ^{2} ∥ w - w_{T}^{*} ∥_{2, [0, T]}^{2} + x_{0}^{T} X (0, T, X_{2}) x_{0},$

(633)

ahol

$u_{*, T} (t) = - B_{2} X (t, T, X_{2}) x (t), w_{*, T} (t) = γ^{- 2} B_{1}^{T} X (t, T, X_{2}) x (t)$

(634)

minden $t \leq T$ -re, következik, hogy

$J (u, w_{*, T}, X_{2}) = x_{0}^{T} X (0, T, X_{2}) x_{0} + ∥ u - u_{*, T} ∥_{2, [0, T]}^{2} \geq x_{0}^{T} X (0, T, X_{2}) x_{0} .$

(635)

Mésrészt az optimális $ℋ_{2}$ szabályozót használva $t > T$ esetén

$\int_{T}^{\infty} z^{T} z d t \geq min_{K} \int_{T}^{\infty} {\tilde{z}}^{T} \tilde{z} d t = x^{T} (T) X_{2} x (T) .$

(636)

Ezért

$∥ z ∥_{2}^{2} - γ^{2} ∥ w ∥_{2}^{2} = \int_{0}^{\infty} (z^{T} z - γ^{2} w^{T} w) d t = \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t + \int_{T}^{\infty} z^{T} z d t$

(637)

felhasználásával következik, hogy

$∥ z ∥_{2}^{2} - γ^{2} ∥ w ∥_{2}^{2} \geq \int_{0}^{T} (z^{T} z - γ^{2} w^{T} w) d t + x^{T} (T) X_{2} x (T) = J (u, w, T, X_{2})$

(638)

minden $w \in ℒ_{2}$ jelre.

Ezen egyenlőtlenségek felhasználásával adódik, hogy

$x_{0}^{T} X (0, T, X_{2}) x_{0} \leq J (u, w_{*, T}, T, X_{2})) \leq ∥ z ∥_{2} - γ^{2} ∥ w_{*, T} ∥_{2}^{2} \leq β ∥ x_{0} ∥^{2}$

(639)

minden $T$ -re. Tehát $X (0, T, X_{2})$ egyenletesen korlátos $T$ -ben.

Az időinvariancia miatt $X (t, T, X_{2}) = X (0, T - t, X_{2})$ , így létezik $β$ , hogy

$x_{0}^{T} X (t, T, X_{2}) x_{0} \leq β ∥ x_{0} ∥^{2}$

(640)

amiből következik, hogy a differenciál Riccati egyenlet megoldásai egyenletesen korlátosak $T$ -ben.

A monotonitás kimutatásához tekintsük a Riccati egyenlet deriváltját

$- \frac{d^{2}}{d t^{2}} X = \dot{X} (A - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X) + {(A - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X)}^{T} \dot{X},$

(641)

ami egy lineáris egyenlet, tehát

$\dot{X} (t, T, X_{2}) = Φ (t, T) \dot{X} (T, T, X_{2}) Φ^{T} (t, T)$

(642)

ahol $Φ$ az $- {(A - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X)}^{T}$ alapmátrixa. A Riccati egyenletből következik, hogy

$- \frac{d}{d t} X (T, T, X_{2}) = X_{2} A + A^{T} X_{2} - X_{2} (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X_{2} + C_{1}^{T} C_{1} =$

$= γ^{- 2} X_{2} B_{1} B_{1}^{T} X_{2},$

(643)

vagyis, $X (t, T, X_{2})$ egy minoton nem növekvő függvény $t$ -ben.

Ahogyan a $ℋ_{2}$ esetben is, az időinvarianciát felhasználva $X (t, T, X_{2}) = X (τ, T - t + τ, X_{2})$ , vagyis $X (t, T, X_{2})$ egy monoton nem csökkenő függvénye $T$ -nek.

Ugyan így, $X (t, T, X_{2}) = X (0, T - t, X_{2})$ , tehát határesetben

$lim_{T \to \infty} X (t, T, X_{2}) = lim_{T - t \to \infty} X (0, T - t, X_{2}) = X_{\infty},$

(644)

ahol $X_{\infty}$ egy konstans mátrix, amire $X_{\infty} \geq 0$ , mivel $X (t, T, X_{2}) \geq 0$ minden $t \leq T$ esetén. Mivel a Riccati egyenlet megoldásai folytonosan függnek a peremfeltételektől

$X_{\infty} = lim_{T \to \infty} X (t, T, X_{2}) = = lim_{T \to \infty} X (t, T_{1}, X (T_{1}, T, X_{2})) =$

$X (t, T_{1}, lim_{T \to \infty} X (T_{1}, T, X_{2})) = X (t, T_{1}, X_{\infty}) .$

(645)

Ezért $X_{\infty}$ kielégíti a $ℋ_{\infty}$ Riccati differencál egyenletet, ahol a peremfeltétel $X (T_{1}, T_{1}) = X_{\infty}$ , azaz

$X_{\infty} A + A^{T} X_{\infty} - X_{\infty} (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X_{\infty} + C_{1}^{T} C_{1} = 0.$

(646)

Kimutattuk tehát, hogy az algebrai Riccati egyenlet megoldásának létezése szükséges a feltétel a $ℋ_{\infty}$ FI szabnályozó létezéséhez, feltéve, hogy $(A, B_{2})$ stabilizálható, $(C_{1}, A)$ párnak nincsenek nem-megfigyelhető módusai a képzetes tengelyen és a Riccati differenciál egyenleteknek van megoldása minden $T$ -re. Kimutatható, hogy ez utóbbi feltátel nem szükséges és a $ℋ_{\infty}$ algebrai Riccati egyenlet stabilizáló megoldásának létezése ekvivalens azzal, hogy a $H$ Hamiltonian mátrixnak nincsenek sajátértékei a képzetes tengelyen.

A továbbiakban az eljárás követi a $ℋ_{2}$ esetben már látottakat: alkalmazva az $u = - B_{2}^{T} X x$ visszacsatolást, a zárt kör

$\dot{x} = (A - B_{2} B_{2}^{T} X) x + B_{1} w,$

(647)

$z = (\begin{array}{l} C_{1} \\ - D_{12} B_{1}^{T} X \end{array}) x .$

(648)

Ki kell mutatni, hogy ez a rendszer stabil. A Riccati egyenletből kapjuk, hogy

$0 = X A + A^{T} X - X (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X + C_{1}^{T} C_{1} + X (B_{2} B_{2}^{T} - B_{2} B_{2}^{T}) X =$

$= X (A - B_{2} B_{2}^{T} X) + {(A - B_{2} B_{2}^{T} X)}^{T} X + γ^{- 2} X B_{1} B_{1}^{T} X + X B_{2} B_{2}^{T} X + C_{1}^{T} C_{1} .$

(649)

Mivel $X \geq 0$ , a $A - B_{2} B_{2}^{T} X$ minden instabik módusa nem megfigyelhető ${(\begin{array}{l} - γ^{- 1} X B_{1} & X B_{2} C_{1}^{T} \end{array})}^{T}$ -re. Legyen $(λ, x)$ az $A - B_{2} B_{2}^{T} X$ egy instabil módusa,

$(A - B_{2} B_{2}^{T} X) x = λ x, X B_{1} = 0, X B_{2} = 0, C_{1} x = 0.$

(650)

Következik, hogy

$(A - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X) x = (A - (B_{2} B_{2}^{T} X) x = λ x,$

(651)

azaz, $(λ, x)$ az $A - (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X$ -nak is egy módusa. De ez a mátrix stabilis, így $A - B_{2} B_{2}^{T} X$ összes módusa stabil és megfigyelhető.

Mivel $A - B_{2} B_{2}^{T} X$ asszimptotikusan stabilis, a KYP lemmából következik, hogy lemma that $∥ ℱ_{ℓ} (P, K) ∥_{\infty} < γ$ if and only létezik $P$ ami kielégíti az alábbi algebrai Riccati egyenletet:

$X (A - B_{2} B_{2}^{T} P) + {(A - B_{2} B_{2}^{T} P)}^{T} X + γ^{- 2} X B_{1} B_{1}^{T} X + P B_{2} B_{2}^{T} P + C_{1}^{T} C_{1} = 0$

(652)

ahol $(A - B_{2} B_{2}^{T} P) - γ^{- 2} B_{1} B_{1}^{T} X$ asszimptotikusan stabilis.Nyílvánvaló, hogy $X = P$ egy megoldás, így $∥ ℱ_{ℓ} (P, K) ∥_{\infty} < γ$ .

13.3. A $H_{\infty}$ OE feladat

Az FI feladat megoldását felhasználhatjuk az OE szűrési feladat megoldásának előállítására. A $ℋ_{2}$ esetben felírt Kalman szűrővel analó módon képzelhetjük el a $ℋ_{\infty}$ szűrőt: míg a Kalman szűrő az állapotbcslést négyzetes középben minimalizállja a Gauss eloszlású bemenetekre nézve, a $ℋ_{\infty}$ szűrő a becslési hiba erősítését egy $γ$ szintnél kisebbre garantálja minden lehetséges korlátos energiájú bemenet esetén.

A $ℋ_{2}$ feladatnál már látott módon az OE rendszer alakja

$P_{O E} (s) = [\begin{array}{l} A & B_{1} & B_{2} \\ C_{1} & 0 & I \\ C_{2} & D_{21} & 0 \end{array}],$

(653)

ahol $A - B_{2} C_{1}$ stabilis. Ekkor $∥ ℱ_{ℓ} (P_{O E}, K_{O E}) ∥_{\infty} < γ$ ha

$K_{O E} (s) = [\begin{array}{l} A + L_{\infty} C_{1} - B_{2} C_{1} & L_{\infty} \\ C_{1} & 0 \end{array}]$

(654)

ahol $L_{\infty} = - Y C_{2}^{T}$ és $Y$ kielégíti az alábbi algebraic Riccati egyenletet

$A Y + Y A^{T} - Y (C_{2}^{T} C_{2} - γ^{- 2} C_{1}^{T} C_{1}) Y + B_{1} B_{1}^{T} = 0.$

(655)

13.4. Egyszerűsített kimenet visszacsatolásos feladat

Lemma 12.1 Egy $P$ rendszer esetén, ahol $z = C_{1} x + D_{12} u$

$∥ ℱ_{ℓ} (P, K) ∥_{\infty} < γ$

(656)

akkor és csak akkor, ha $(u - u_{*, T}) = U (w - w_{*, T})$ ahol $∥ U ∥_{\infty} < γ$ .

Bizonyítás 12.1 Az $u_{*, T} = - B_{2}^{T} X x$ irányítással, ahol $X$ kielégíti a $ℋ_{\infty}$ FI feladat algebrai Riccati egyenletét, $∥ T_{w z} ∥_{\infty} < γ$ , ahol $T_{w z}$ a $w$ -ről $z$ -re vett átviteli függvény.

A véges horizontú feladatra

$∥ T_{w z} ∥_{[0, T]} < γ \Leftrightarrow J (K, w, T, Ψ) < - ε ∥ w ∥_{2, [0, T]}^{2}$

(657)

és

$J (K, w, T, Ψ) = ∥ u - u_{*, T} ∥_{2, [0, T]}^{2} - γ^{2} ∥ w - w_{*, T} ∥_{2, [0, T]}^{2} .$

(658)

Legyen $L$ a $w$ jelet $w - w_{*, T}$ -re képző rendszer:

$L (s) = [\begin{array}{l} A - B_{2} B_{2}^{T} X & B_{1} \\ - γ^{- 2} B_{1}^{T} X & I \end{array}] .$

(659)

Ha $∥ U ∥_{[0, T]} < γ$ , akkor létezik $ε$ , hogy

$J (K, w, T, Ψ) = ∥ U (w - w_{*, T}) ∥_{2, [0, T]}^{2} - γ^{2} ∥ w - w_{*, T} ∥_{2, [0, T]}^{2} \leq$

$\leq (∥ U ∥_{[0, T]}^{2} - γ^{2}) ∥ w - w_{*, T} ∥_{2, [0, T]}^{2} =$

$= (∥ U ∥_{[0, T]}^{2} - γ^{2}) ∥ L w ∥_{2, [0, T]}^{2} \leq - ε ∥ w ∥_{2, [0, T]}^{2},$

(660)

azaz, $∥ ℱ_{ℓ} (P, K) ∥_{[0, T]} < γ$ .

Fordítva, ha $∥ ℱ_{ℓ} (P, K) ∥_{[0, T]} < γ$ , akkor

$∥ U (w - w_{*, T}) ∥_{2, [0, T]}^{2} - γ^{2} ∥ w - w_{*, T} ∥_{2, [0, T]}^{2} \leq - ε ∥ w ∥_{2, [0, T]}^{2} \leq$

$\leq - ε ∥ L^{- 1} (w - w_{*, T}) ∥_{2, [0, T]}^{2} \leq - \frac{ε}{∥ L ∥_{[0, T]}^{2}} ∥ w - w_{*, T} ∥_{2, [0, T]}^{2} < 0,$

(661)

amiből következik, hogy $∥ U ∥_{[0, T]} < γ$ .

Ebből az eredményből kiindulva írjul át az eredeti $P$ rendszert a $ℋ_{2}$ esethez hasonlóan két rendszer, $\hat{P}$ és $P_{t m p}$ , Redheffer szorzataként:

$\hat{P} (s) = [\begin{array}{l} A + B_{2} F_{\infty} & B_{1} & B_{2} \\ C_{1} + D_{12} F_{\infty} & 0 & D_{12} \\ - γ^{- 2} B_{1}^{T} X & I & 0 \end{array}],$

(662)

$P_{t m p} (s) = [\begin{array}{l} A + γ^{- 2} B_{1} B_{1}^{T} X & B_{1} & B_{2} \\ - F_{\infty} & 0 & I \\ C_{2} & D_{21} & 0 \end{array}]$

(663)

ahol

$v = u - u_{*, T} = u + B_{2}^{T} X x, r = w - w_{*, T} = w - γ^{- 2} B_{1}^{T} X x .$

(664)

Mivel $ℱ_{ℓ} (P, K) = ℱ_{ℓ} (\hat{P}, ℱ_{ℓ} (P_{t m p}, K))$ és a $\hat{P}$ által generált jel $z = (C_{1} + D_{12} F_{\infty}) x + D_{12} u$ , következik, hogy

$∥ ℱ_{ℓ} (P, K) ∥_{[0, T]} < γ \Leftrightarrow ∥ ℱ_{ℓ} (P_{t m p}, K) ∥_{[0, T]} < γ,$

(665)

ami a $T \to \infty$ határesetben is igaz marad.

$P_{t m p}$ egy OE típusú feladatot határoz meg a hozzá tartozó

$K (s) = [\begin{array}{l} A_{t m p} + L_{\infty} C_{2} + B_{2} F_{\infty} & L_{\infty} \\ - F_{\infty} & 0 \end{array}]$

(666)

szabáltozóval, ahol $A_{t m p} = A + γ^{- 2} B_{1} B_{1}^{T} X$ és ahol $L_{\infty} = - Z C_{2}^{T}$ és $Z$ kielégíti az

$A_{t m p} Z + {ZA}_{t m p}^{T} - Z (C_{2}^{T} C_{2} - γ^{- 2} F_{\infty}^{T} F_{\infty}) Z + B_{1} B_{1}^{T} = 0$

(667)

algebrai Riccati egyenletet.

Figyeljük meg, hogy a $ℋ_{2}$ esettel ellentétben a $ℋ_{\infty}$ probléma két algebrai Riccati egyenlete nem független egymástól: $F_{\infty} = - B_{2}^{T} X$ -ben az $X$ mátrix az FI Riccati egyenlet megoldása.

Ha megköveteljük azonban, hogy $ρ (X Y) < γ^{2}$ , vagyis $I - γ^{- 2} X Y$ invertálható, akkor az

$Y = Z {(I + γ^{- 2} X Z)}^{- 1}$

(668)

transzformáció invertálható és $Z$ akkor és csak akkor elégíti ki az OF Riccati egyenletet ha $Y$ megoldása az

$A Y + Y A^{T} + B_{1} B_{1}^{T} - Y (C_{2}^{T} C_{2} - γ^{- 2} C_{1}^{T} C_{1}) Y = 0$

(669)

OE algebrai Riccati egyenletnek.

Összegzésként az egyszerüsített kimenet visszacsatolásos feladat megoldását az alábbi algoritmus írja le:

Tétel 12.1 Az egyszerüsített OF feladat megoldása

$K_{O F} (s) = [\begin{array}{l} A_{\infty} & L_{\infty} \\ - F_{\infty} & 0 \end{array}]$

(670)

ahol

$A_{\infty} = A + γ^{- 2} B_{1} B_{1}^{T} X - Z C_{2}^{T} C_{2} - B_{2} B_{2}^{T} X,$

(671)

$L_{\infty} = - Z C_{2}^{T}, F_{\infty} = - B_{2}^{T} X,$

(672)

$X A + A^{T} X - X (B_{2} B_{2}^{T} - γ^{- 2} B_{1} B_{1}^{T}) X + C_{1}^{T} C_{1} = 0,$

(673)

$Y A^{T} + A Y - Y (C_{2}^{T} C_{2} - γ^{- 2} C_{1}^{T} C_{1}) Y + B_{1} B_{1}^{T} = 0,$

(674)

$Z = Y {(1 - γ^{- 2} X Y)}^{- 1} .$

(675)

Vissza		Előre
12. fejezet - H2 irányítások tervezése	Főoldal	14. fejezet - Rekonfiguráló és hibatűrő irányítások tervezése

13. fejezet - Hinf. szabályozók tervezése

13.1. Véges horizontú FI feladat

13.2. Végtelen horizontú FI feladat

13.3. A H ∞ OE feladat

13.4. Egyszerűsített kimenet visszacsatolásos feladat

13.3. A $H_{\infty}$ OE feladat